Narysuj na płaszczyźnie zespolonej: asdf: Narysuj na płaszczyźnie zespolonej: z* − sprzężenie Im(z²) ≥ Re((z*)²) Próbowałem na postać trygonometrczyną ale bez skutku Prosze o wskazówki

ABC: z=x+yi z²=x²+2xyi−y² Im z²=2xy z*=x−yi z*²=x²−2xyi−y² Re (z*²)=x²−y² x²−y²≤2xy przy czym zauważ że x²−y²−2xy=0 to równanie pary prostych przecinających się (x−y)²−2y²=0

asdf: Dziekuje bardzo, mógłbyś mi pokazać jak przez postać trygonometryczną takie robić? Bo mam pare nastepnych zadań i są tam potęgi większa, więc algebraicznie odpada raczej

asdf: Chociaż właściwie udałło mi sie teraz, możesz olać. Jedyne co wymaga wytłumaczenia to te 2 proste na końcu, jak i skąd?

ABC: pokaż jakieś z tymi wyższymi potęgami to się zobaczy, od postaci tryg. to są tu lepsi spece niż ja, ale mogę się wypowiedzieć czy istotnie algebraicznie się nie da.

ABC: 2 proste na końcu a²−b²=(a−b)(a+b)

asdf: A choćby to samo tylko do 5 potegi na przykład Im(z⁵) ≥ Re((z*)⁵)

asdf: Pierwszy raz widze takie równanie dwóch prostych

ABC: No , takie algebraicznie trochę trudniej.

ABC: to jest typu (y−x)(y+x)=0 czyli y=x lub y=−x co w tym trudnego?

asdf: (x−y)²−2y²=0 Aaa dobra, nie ogarnąłem. Dzięki!

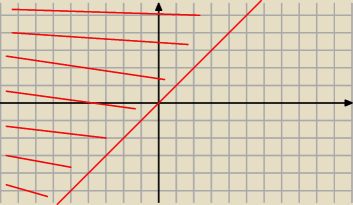
Adamm: u = z⁵ Im(u) ≥ Re(u^*) Im(u) ≥ Re(u) wystarczy spojrzeć na okrąg jednostkowy

Adamm: będzie to suma 5 kątów

asdf: Okej, postaram się pokombinować