f kwadratowa
dusiamatmusiac2497: Rozwiąż równanie |x2+4x−5|+|x2+4x|=5
Bardzo proszę o rozpisanie tego przykładu (w szczególności przypadki)
Odpowiedź x∈<−5;−4>∪<0;1>
Rozpisałam na osi dla: −5 i −4, −5 i 0, 0 i 1, −4 i 1. Wychodzi mi przedział od 0 do 1
domknięty oraz punkt 4.
Nie wiem gdzie mam błąd. Czy ktoś może rozwiązać, szczególnie te przypadki z −5?
23 lis 18:33
Eta:
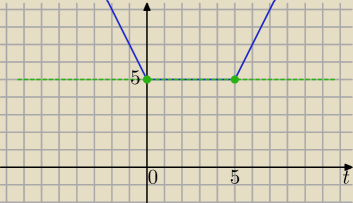
Podstawienie : x
2+4x=t
|t−5|+|t|=5 −−− wykres niebieski
t∊<0,5>
to x
2+4x≥0 i x
2+4x≤5
x∊(−
∞, −4>U <0,
∞) i x∊<−5,1>
Odp: x∊<−5,−4> U <0,1>
=====================
23 lis 18:53
Mila:
|x
2+4x−5|+|x
2+4x|=5
x
2+4x−5≥0
Δ=6
2
x
1=−5 lub x
2=1
x≤−5 lub x≥1
x
2+4x≥0⇔x*(x+4)≥0
x
1=0 lub x
2=−4
1) |x
2+4x−5|=x
2+4x−5 dla x≤−5 lub x≥1
w tych przedziałach |x
2+4x|=x
2+4x
wtedy mamy równanie:
x
2+4x−5+x
2+4x=5
2x
2+8x−10=0
x
2+4x−5=0
x=−5 lub x=1
lub
2) x∊(−5,−4> ∪<0,1) mamy równanie:
−x
2−4x+5+x
2+4x=5
5=5 ⇔
każda liczba x∊(−5,−4> ∪<0,1) spełnia równanie
lub
3) x∊(−4,0) obydwa wyrażenia są ujemne, to mamy równanie:
−x
2−4x+5−x
2−4x=5
x=0 lub x=−4 nie należą do otwartego przedziału
odp.
(1 i 2)
x∊<−5,−4> ∪<0,1>
============
23 lis 18:58
ABC: x2+4x−5=(x−1)(x+5)
x2+4x=(x−0)(x+4)
stąd dla dowolnego x takiego że −5≤x≤−4 masz równanie
−(x2+4x−5)+(x2+4x)=5
i staje się ono prawdziwą tożsamością 5=5
23 lis 18:58
PW:
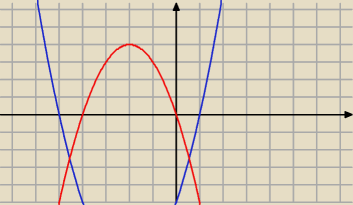
Rysunek powinien być ostatnim elementem rozwiązania.
Jak wiadomo dla dowolnych rzeczywistych a, b
(1) |a + b| ≤ |a| + |b|,
przy czym równość ma miejsce wtedy i tylko wtedy, gdy ab ≥ 0.
Zadanie można zapisać w postaci
|x
2+4x−5| + |−x
2−4x| = 5.
Stosując nierówność (1) otrzymamy
|x
2+4x−5−x
2−4x| ≤ |x
2+4x−5| + |−x
2−4x| = 5,
skąd
|−5| ≤ |x
2+4x−5| + |−x
2−4x| = 5,
przy czym równość ma miejsce tylko wtedy, gdy x
2+4x−5 i −x
2−4x są jednakowych znaków.
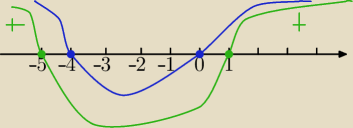
Dla sporządzenia wykresów przekształcamy x
2+4x−5 = (x−1)(x+5), −x
2−4x = −x(x+4) i z
rysunku odczytujemy przedziały, na których funkcje mają jednakowe znaki lub jedna z nich
przyjmuje wartość 0 − dzieje się tak na <−5, −4>∪<0, 1>.
23 lis 22:41
Eta:

23 lis 23:47
 Podstawienie : x2+4x=t
|t−5|+|t|=5 −−− wykres niebieski
t∊<0,5>
to x2+4x≥0 i x2+4x≤5
x∊(−∞, −4>U <0,∞) i x∊<−5,1>
Odp: x∊<−5,−4> U <0,1>
=====================
Podstawienie : x2+4x=t
|t−5|+|t|=5 −−− wykres niebieski
t∊<0,5>
to x2+4x≥0 i x2+4x≤5
x∊(−∞, −4>U <0,∞) i x∊<−5,1>
Odp: x∊<−5,−4> U <0,1>
=====================
 |x2+4x−5|+|x2+4x|=5
x2+4x−5≥0
Δ=62
x1=−5 lub x2=1
x≤−5 lub x≥1
x2+4x≥0⇔x*(x+4)≥0
x1=0 lub x2=−4
1) |x2+4x−5|=x2+4x−5 dla x≤−5 lub x≥1
w tych przedziałach |x2+4x|=x2+4x
wtedy mamy równanie:
x2+4x−5+x2+4x=5
2x2+8x−10=0
x2+4x−5=0
x=−5 lub x=1
lub
2) x∊(−5,−4> ∪<0,1) mamy równanie:
−x2−4x+5+x2+4x=5
5=5 ⇔każda liczba x∊(−5,−4> ∪<0,1) spełnia równanie
lub
3) x∊(−4,0) obydwa wyrażenia są ujemne, to mamy równanie:
−x2−4x+5−x2−4x=5
x=0 lub x=−4 nie należą do otwartego przedziału
odp.
(1 i 2)
x∊<−5,−4> ∪<0,1>
============
|x2+4x−5|+|x2+4x|=5
x2+4x−5≥0
Δ=62
x1=−5 lub x2=1
x≤−5 lub x≥1
x2+4x≥0⇔x*(x+4)≥0
x1=0 lub x2=−4
1) |x2+4x−5|=x2+4x−5 dla x≤−5 lub x≥1
w tych przedziałach |x2+4x|=x2+4x
wtedy mamy równanie:
x2+4x−5+x2+4x=5
2x2+8x−10=0
x2+4x−5=0
x=−5 lub x=1
lub
2) x∊(−5,−4> ∪<0,1) mamy równanie:
−x2−4x+5+x2+4x=5
5=5 ⇔każda liczba x∊(−5,−4> ∪<0,1) spełnia równanie
lub
3) x∊(−4,0) obydwa wyrażenia są ujemne, to mamy równanie:
−x2−4x+5−x2−4x=5
x=0 lub x=−4 nie należą do otwartego przedziału
odp.
(1 i 2)
x∊<−5,−4> ∪<0,1>
============
 Rysunek powinien być ostatnim elementem rozwiązania.
Jak wiadomo dla dowolnych rzeczywistych a, b
(1) |a + b| ≤ |a| + |b|,
przy czym równość ma miejsce wtedy i tylko wtedy, gdy ab ≥ 0.
Zadanie można zapisać w postaci
|x2+4x−5| + |−x2−4x| = 5.
Stosując nierówność (1) otrzymamy
|x2+4x−5−x2−4x| ≤ |x2+4x−5| + |−x2−4x| = 5,
skąd
|−5| ≤ |x2+4x−5| + |−x2−4x| = 5,
przy czym równość ma miejsce tylko wtedy, gdy x2+4x−5 i −x2−4x są jednakowych znaków.
Dla sporządzenia wykresów przekształcamy x2+4x−5 = (x−1)(x+5), −x2−4x = −x(x+4) i z
rysunku odczytujemy przedziały, na których funkcje mają jednakowe znaki lub jedna z nich
przyjmuje wartość 0 − dzieje się tak na <−5, −4>∪<0, 1>.
Rysunek powinien być ostatnim elementem rozwiązania.
Jak wiadomo dla dowolnych rzeczywistych a, b
(1) |a + b| ≤ |a| + |b|,
przy czym równość ma miejsce wtedy i tylko wtedy, gdy ab ≥ 0.
Zadanie można zapisać w postaci
|x2+4x−5| + |−x2−4x| = 5.
Stosując nierówność (1) otrzymamy
|x2+4x−5−x2−4x| ≤ |x2+4x−5| + |−x2−4x| = 5,
skąd
|−5| ≤ |x2+4x−5| + |−x2−4x| = 5,
przy czym równość ma miejsce tylko wtedy, gdy x2+4x−5 i −x2−4x są jednakowych znaków.
Dla sporządzenia wykresów przekształcamy x2+4x−5 = (x−1)(x+5), −x2−4x = −x(x+4) i z
rysunku odczytujemy przedziały, na których funkcje mają jednakowe znaki lub jedna z nich
przyjmuje wartość 0 − dzieje się tak na <−5, −4>∪<0, 1>.
