nierówność z argumentem liczby zespolonej
asdf: Jak to narysować

π ≤ arg(z* − i − 1) ≤
32π
23 lis 11:25
ABC: * to sprzężenie? jeśli tak to proste jest, oznacz z=x+yi, wtedy z*=x−yi
23 lis 11:28
asdf: Tak, sprzężenie.
π ≤ arg( x−1 −(y + 1)i ) ≤
32π
Coś kojarzy mi sie przesunięcie o wektor, ale nie wiem jak to zrobic

gdy by było :
π ≤ arg( z) ≤
32π
To by to była 3 ćwiartka, a jak i w którą stronę przesunąć to już sam nie wiem
23 lis 11:35
ABC: mieliście podane jakieś wzory na arg z? przez arc tangens np.?
23 lis 11:39
asdf: Nie, takich rzeczy nie było
23 lis 12:10
Pytający:
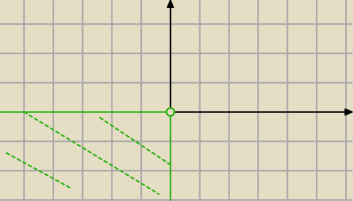
23 lis 14:28
Pytający:
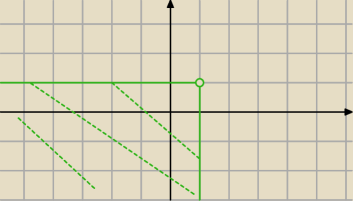
| | 3π | |
π ≤ arg(z − (i+1)) ≤ |
| |
| | 2 | |
23 lis 14:28
Pytający:
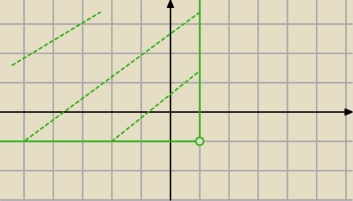
| | 3π | |
π ≤ arg(z* − i − 1) ≤ |
| // z |
| | 2 | |
23 lis 14:28
Rivit: Dzięki wielkie, a jeszcze pytanie mam.
Bo tu chyba kolejność przekształceń nie ma znaczenia. Czy ogólnie przy tego typu operacjach
jest przyjęta jakaś kolejność czy zawsze będzie tak samo wychodzisz niezależnie od tego czy
najpierw przesune o wektor a potem sprzężenie?
23 lis 14:31
Pytający:
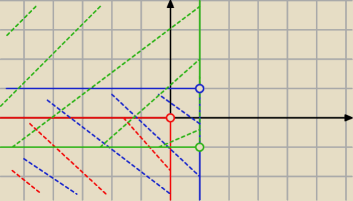
Można w innej kolejności, ale tak samo trzeba myśleć, co się robi/rysuje.

Zauważ, że
z na każdym rysunku wyżej to co innego (mogłem chociaż innego koloru użyć).
Może tu będzie to jaśniejsze:
| | 3π | |
π≤arg(z* − (i+1))≤ |
| // z* − (i+1)+(i+1)=z* |
| | 2 | |
| | 3π | |
π≤arg(z* − (i+1))≤ |
| // (z*)*=z |
| | 2 | |
Trzeba pamiętać, że jak rysujesz "sprzężony wykres", to robisz sprzężenie całości, a nie tylko
zet czy innej zmiennej.
23 lis 16:00
Pytający:
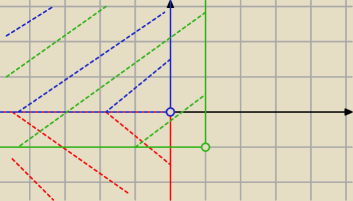
I inna kolejność:
| | 3π | |
π≤arg((z−(−i+1))*)≤ |
| // (z*−(i+1))*=(z*)*−(i+1)*=z−(−i+1) |
| | 2 | |
| | 3π | |
π≤arg((z−(−i+1))*)≤ |
| // z−(−i+1)+(−i+1)=z |
| | 2 | |
Trzeba pamiętać, że jak rysujesz "sprzężony wykres", to robisz sprzężenie całości, a nie tylko
zet czy innej zmiennej.
23 lis 16:03
Rivit: Dziękuję bardzo!
24 lis 09:17
 π ≤ arg(z* − i − 1) ≤ 32π
π ≤ arg(z* − i − 1) ≤ 32π
 gdy by było :
π ≤ arg( z) ≤ 32π
To by to była 3 ćwiartka, a jak i w którą stronę przesunąć to już sam nie wiem
gdy by było :
π ≤ arg( z) ≤ 32π
To by to była 3 ćwiartka, a jak i w którą stronę przesunąć to już sam nie wiem



 Można w innej kolejności, ale tak samo trzeba myśleć, co się robi/rysuje.
Można w innej kolejności, ale tak samo trzeba myśleć, co się robi/rysuje.  Zauważ, że z na każdym rysunku wyżej to co innego (mogłem chociaż innego koloru użyć).
Może tu będzie to jaśniejsze:
Zauważ, że z na każdym rysunku wyżej to co innego (mogłem chociaż innego koloru użyć).
Może tu będzie to jaśniejsze:
 I inna kolejność:
I inna kolejność: