Liczby zespolone interpretacja geometryczna
simon5005: Przedstaw interpretację geometryczną zbioru:
| | π | |
{z∊C: 0 ≤ Arg z2 ≤ |
| , |z+2−i| < |z−2+i| } |
| | 3 | |
Arg z
2 = 2φ − 2kπ k∊{0,1} φ∊<0;2π)
Rozwiązujemy to podstawiając k = 0 i k = 1 i interpretacją geometryczną będzie suma obszarów
pomiędzy danymi półprostymi. Dla k =1 mamy sprzeczność.
Teraz:
|z −(−2+i)| < |z−(2−i)|
Jak to zinterpretować? Wiem, że w przypadku gdy te moduły są równe to mamy symetralną prostej
na której
leżą te punkty z modułu.
Jak powinno wyglądać rozwiązanie?
Mila:
I sposób
|z+2−i| < |z−2+i|
x=x+iy, x,y∊R
|(x+2)+i*(y−1)|< |(x−2)
2+i*((y+1)|
(x+2)
2+(y−1)
2<(x−2)
2+(y+1)
2⇔
y>2x
Półpłaszczyzna nad prostą y=2x
II sposób
|z −(−2+i)| < |z−(2−i)|
1) piszemy równanie symetralnej odcinka o końcach
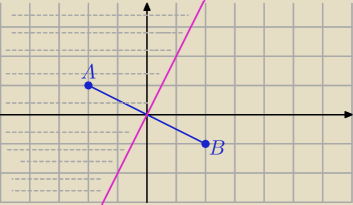
A=(−2,1) B=(2,−1)
| | 1 | |
Prosta AB: y=ax, i 1=a*(−2)⇔a=− |
| |
| | 2 | |
Symetralna AB:
s: y=2x
|z+2−i| < |z−2+i| musisz wybrać półpłaszczyznę
Ja sprawdzam wybierając jeden punkt
P=(−2,0)
|−2+2−i|< ?|−2−2+i|
|i|<|−4+i|
1<
√16+1
czyli nad prostą y=2x
 I sposób
|z+2−i| < |z−2+i|
x=x+iy, x,y∊R
|(x+2)+i*(y−1)|< |(x−2)2+i*((y+1)|
(x+2)2+(y−1)2<(x−2)2+(y+1)2⇔
y>2x
Półpłaszczyzna nad prostą y=2x
II sposób
|z −(−2+i)| < |z−(2−i)|
1) piszemy równanie symetralnej odcinka o końcach
A=(−2,1) B=(2,−1)
I sposób
|z+2−i| < |z−2+i|
x=x+iy, x,y∊R
|(x+2)+i*(y−1)|< |(x−2)2+i*((y+1)|
(x+2)2+(y−1)2<(x−2)2+(y+1)2⇔
y>2x
Półpłaszczyzna nad prostą y=2x
II sposób
|z −(−2+i)| < |z−(2−i)|
1) piszemy równanie symetralnej odcinka o końcach
A=(−2,1) B=(2,−1)