Wykres funkcji i obliczenie punktów + opis Maciek:

	1		2
Wykonaj wykres funkcji f(x)=		x+		obliczając punkty przecięcia wykresu z osiami
	2		3

układu współrzędnych. Opisz własności funkcji na podstawie otrzymanego wykresu.

6latek: D_f= R Z_wf=R funkcja jest funkcja rosnaca

	2
Z osia OY od razu ze wzoru (0,		)
	3

	1		2
Z osia OX wsporzedna y=0 a wxplorzedna x wylicz 0=		x+
	2		3

masz dwa punkty rob wykres

Maciek: Nie bardzo wiem co i jak, a muszę mieć to wszystko ładnie rozpisane :x

6latek: To znaczy czego tutaj nie rozumiesz ? Co ci da ladne rozpisanie ?

	1		2
Nie potrafisz rozwiazac prostego rownania		x+		=0 ?
	2		3

Jerzy: Monotoniczność nie ma znaczenia. Tak jak pokazał małolat, aby napisać wzór funkcji liniowej, trzeba znać dwa punkty przez które przechodzi wykres.

Eta:

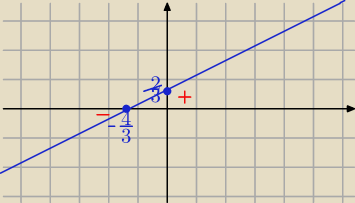
	−b
y=ax+b POy(0,b) , POx(		,0) dla a>0 −− funkcja rosnąca
	a

	1		2		1		2
y=		x+		a=		>0 −−− f. rosnąca , b=
	2		3		2		3

	2		−4		4
POy(0,		) , POx(		,0) to miejsce zerowe x= −
	3		3		3

Własności: Dziedziną jest R Zbiorem wartości R f.rosnąca

	2
POy(0,
	3

	−4
POx(		)
	3

	−4
xo=
	3

	−4
f(x) >0 ⇔ x∊ (		,+∞)
	3

	−4
f(x)<0 ⇔ x∊(−∞,		)
	3

Maciek: Skąd się wzięło to P_OX⁻⁴₃? Możesz zapisać?

Eta:

	−b
POx(		,0)
	a

−b		2   −   3
	=		= ......
a		1   2

Eta: Maciek = vi ?