| x3+1 | ||
Funkcja f określona jest wzorem f(x)= | . Wykaż, że jeżeli dla dwóch ujemnych | |
| x2 |
| a3+1 | b3+1 | |||
= | a,b ≠ 0 | |||
| a2 | b2 |
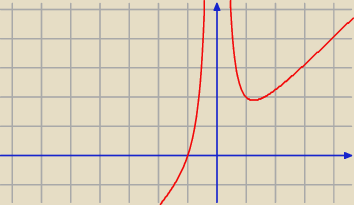 Poprawnie.
Można było obliczyć pochodną funkcji f(x)=x+x−2 i zauważyć, że f jest funkcją rosnącą dla
x<0. Ciut szybciej.
Na rysunku wykres f, ale tego nie musieliśmy robić, jedynie pokazać rachunkiem, że f'(x)>0 dla
x<0.
Poprawnie.
Można było obliczyć pochodną funkcji f(x)=x+x−2 i zauważyć, że f jest funkcją rosnącą dla
x<0. Ciut szybciej.
Na rysunku wykres f, ale tego nie musieliśmy robić, jedynie pokazać rachunkiem, że f'(x)>0 dla
x<0.
 Jeszcze nie umiem pochodnych ale gdy je sobie ogarnę to wrócę do Twojej wskazówki
Jeszcze nie umiem pochodnych ale gdy je sobie ogarnę to wrócę do Twojej wskazówki 