stereometria Yano: Dany jest ostrosłup prawidłowy trójkątny ABCS, w którym długość krawędzi podstawy jest równa 4. Ostrosłup ten przecięto płaszczyzną BCD, która przechodzi przez krawędź podstawy BC i jest prostopadła do przeciwległej krawędzi bocznej ostrosłupa. Płaszczyzna przekroju odcina ostrosłup ABCD, którego objętość jest cztery razy mniejsza od objętości ostrosłupa ABCS. Oblicz długość krawędzi bocznej ostrosłupa ABCS.

Mila: Masz może odpowiedź do tego zadania?

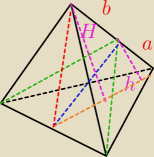
Blee: Z treści zadania (proporcja objętości) wynika, że 4h = H Z proporcji trójkątów: 4a = b I teraz: b² + x² = y² a² + x² = z² gdzie:

	4√3
z =		= 2√3 (wysokość trójkąta równobocznego)
	2

b = 4a y = √(a+b)² − 2² = √25a² − 4 i sprowadza się do układu równań z dwoma niewiadomymi (a i x) wyznaczasz i będzie z górki.

Yano: Serdecznie dziękuję Mila (jak zawsze wspaniałe rowiązanie)

Mila: No, nie wiem, czy to dobry wynik (mogłam się pomylić), gdzieś powinien być i internecie. Może Eta też policzy. Są inne sposoby. Może Jutro napiszę.

Tadeusz:

	h		1		1
chyba jednak		=		a nie
	H		4		5

Mila: Jest błąd. Poprawiam

Mila: O widzę Tadeusza, pozdrawiam.

Tadeusz: serdeczności Milu

Mila: Yano,źle przeczytałam treść i rozwiązałam inne zadanie, zresztą popełniłam tam pomyłkę:

Eta: Według moich obliczeń długość krawędzi bocznej ABCS : b=4√2 ======

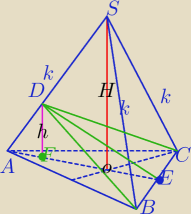
Mila: a=4, DE⊥AS 1)

	1
VABCD=		VABCS⇔H=4h
	4

(ostrosłupy mają tę samą podstawę) 2)

	4√3
|AE|=2√3, |AO|=
	3

3)

	1
ΔAFD∼ΔAOS w skali k=		⇔
	4

AF		1		AD		1
	=		i		=
AO		4		AS		4

	1
|AF|=		|AO|, |AS|=4|AD|=4d
	4

	1		4√3		√3
|AF|=		*		=
	4		3		3

	√3		5√3
|EF|=2√3−		=
	3		3

4)W prostokątnym ΔADE: h²=|AF|*|FE|

	√3		5√3		5
h2=		*		, h2=
	3		3		3

h²+|AF|²=d²

	5		1
d2=		+
	3		3

d²=2 d=√2 |AS|=k=4√2 ========== Mam nadzieję, że już nie ma pomyłki. Liczył ktoś?

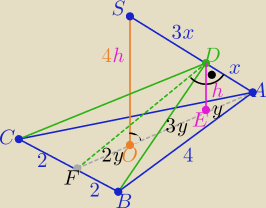
Eta: 1/ Z treści zadania H=4h 2/ trójkaty OAS i EAD są podobne z cechy (kkk) w skali k=4

	4√3		√3		5√3
3/ |AF|=6y =		⇒ 6y=2√3 ⇒ y=|EA|=		i 5y=|FE|=
	2		3		3

4/ w trójkącie FAD prostokątnym ( z treści zadania)

	5
h2=|FE|*|EA| ⇒ h2=
	3

4/ w ΔEAD : x²=h²+y² ⇒ x²= 2 ⇒ x=√2 zatem |AS|=4x= 4√2 ===========

Mila: Jesteś Eto niezawodna, ślicznie dziękuję W poprzedniej wersji zinterpretowałam, że objętość górnego czworościanu jest 4 razy większa od dolnego. Rachunki były nieprzyjazne.

Eta:

Mila: A Yano nie zagląda tutaj