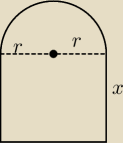
Zadanie maksymalizacyjne - Proszę o pomoc Kitten: Proszę o pomoc przy tym zadaniu. Fabryka produkująca okna ma w swojej ofercie okna zakończone u góry pókolem, tzn. okno do pewnej wysokości ramy ma kształt prostokątny, a na górze półkole. Jak dobrać wysokość odcinka od dołu ramy do półkola (a) i promień koła (r) dot. półkola, tak aby uzyskać jak największe pole powierzchni okna, przy jak najmniejszym obwodzie ramy. | −−−−−−− | | r | a | | _________ (tak wygląda dolna część okna − górę zamyka półkole

Basia: sprawdź treść tego zadania; nie ma tam być przy zadanym obwodzie ramy?

Kitten: Przepraszam, jest przy DANYM obwodzie k. Jakiś pomysł co dalej?

Basia: x,r>0

	πr2
P=2xr+
	2

L = 2x+2r+πr 2x = L−2r−πr

	πr2		πr2
P(x) = (L−2r−πr)r +		= Lr − (2+π)r2 +		=
	2		2

	1		π
r2(		π−2−π)+Lr = (−		−2)r2 + Lr
	2		2

	π		π
P'(x) = 2(−		−2)r + L = −2(		+2)r+L
	2		2

	L		2L
P'(x) = 0 ⇔ r =		=
	π   +2 2		π+4

łatwo już pokazać, że w tym punkcie P(x) osiąga maksimum

Kitten: Dziękuję ślicznie

Kitten: Dziękuję serdecznie!

Basia: Na zdrowie