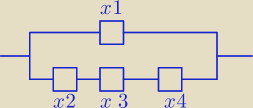
Prawdopodobieństwo simon5005: Układ składa się z 4 jednakowych bloków, które ulegają uszkodzeniu niezależnie od innych. Prawdopodobieństwo poprawnego działania poszczególnego bloku w ciągu doby wynosi 0,85. Wyznacz prawdopodobieństwo bezawaryjnej pracy układu przez całą dobę. A − układ działa poprawnie (przesyła sygnał z jednego do drugiego końca) Zdarzenie przeciwne do A − układ nie działa Czyli w P(A') na pewno nie działa x1 oraz nie działa co najmniej jeden z trójki x2,x3,x4. Jeśli tok mojego rozumowania jest dobry proszę o sposób, żeby obliczyć P(A'), a jeśli jestem w błędzie proszę o poprawne rozwiązanie.

Blee: P(A') = 0.15*(0.15³ + 3*0.15²*0.85 + 3*0.15*0.85²) = ...

Blee: ale to lepiej policzyć P(A) P(A) = 0.85 + 0.85³ − 0.85⁴ czyli: x₁ działa całą dobę + x₂,x₃,x₄ działają całą dobę − x₁,x₂,x₃,x₄ działają całą dobę

Adamm: jest ok

ABC: mozna tez tak dol dziala 0.85³ gora dziala 0.85 dol nie dziala 1−0.85³ gora nie dziala 1−0.85 dol nie dziala i gora nie dziala (1−0.85³)(1−0.85) dol dziala lub gora dziala 1−(1−0.85³)(1−0.85) jakby nie liczyc pstwo dzialania okolo 0.94

simon5005: Dziękuję za wszystkie odpowiedzi, faktycznie trochę sobie utrudniłem życie licząc P(A') zamiast P(A), , ale na to nie wpadłem