21 lis 20:18
Maciess: 11.
Jeśli W (x) jest podzielny przez x2+x−6 to oznacza, że jednymi z z jego pierwiastków są 2 i
−3?
21 lis 20:28
iteRacj@: tak
21 lis 20:33
the foxi:
dziękuję za udostępnienie, widzę że nie była zbyt wymagająca
bardzo mi się spodobało zadanie 8.
| | 3 | |
sin(x+30o)+sin(90o−x)= |
| , x∊[0;360o] |
| | 2 | |
| | x+30o+90o−x | | x+30o−90o+x | | 3 | |
2sin |
| cos |
| = |
| |
| | 2 | | 2 | | 2 | |
...
x∊{0; 60
o; 360
o}
jak natomiast ruszyć zadanie nr 10?
21 lis 21:01
Karol: próbowałem z tw cosinusów ale coś nie wyszło
21 lis 21:07
the foxi:
też o tym myślałem.
| | ⎧ | a2=b2+c2−2bccos(2β) | |
| − | ⎩ | b2=a2+c2−2accosβ |
|
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
a
2−b
2=b
2+c
2−2bccos(2β)−a
2−c
2+2accosβ
cos(2β)=2cos
2β−1
a
2−b
2=b
2−2bc(2cos
2β−1)−a
2+2accosβ
a
2−b
2=a
2+c
2−2accosβ−2bc(2cos
2β−1)−a
2+2accosβ
a
2−b
2=c
2−2bc(2cos
2β−1)
i tutaj się zatrzymałem...
21 lis 21:16
Eta:
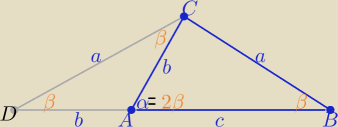
Jeżeli α=2β to ΔDBC i Δ DAC są równoramiennymi i podobnymi z cechy (kkk)
| | a | | b | |
zatem |
| = |
| ⇒ a2=b2+bc ⇒ a2−b2=bc |
| | b+c | | a | |
c.n.w
21 lis 21:19
the foxi:
achhh, podobieństwo, zło wcielone
dziękuję, chyba czas w końcu ujarzmić ten trudny temat...
21 lis 21:22
Eta:
21 lis 21:22
Leszek: Mozna na podstawie twierdzenia sinusow , ale jest wiecej liczenia niz w sposobie @Eta !
21 lis 21:23
Eta:
Zobacz w kluczu odpowiedzi .......................
jak się namęczyli
21 lis 21:24
21 lis 21:27
dde: W zadaniu 15 jedna z odpowiedzi wynosi y=√17x−18. Dlaczego jezeli przyrównam to do 1/4x2+1
to wychodzi że nie mają wspolnego punktu?
21 lis 21:28
dde: O jej. Tam jest 1/4x
2−1
21 lis 21:30
Leszek: Ja zrobilem tylko z tw. Sinusow i nie jest to tak duzo .
a/sin 2β= 2R , b/sin β = 2R ,
Po podstawieniu do tezy a2 − b2 = bc , i rozpisaniu sin 2β = 2 sin β cos β
nie ma tak duzo pisania jak w kluczu , ale @Eta ma palme pierwszenstwa ! ! !
21 lis 21:33
Mila:
Ja też zrobiłam z tw. sinusów, i prościej niż w kluczu.
Nawet nie trzeba rozpisywać sin2β.
Popatrzyłam, że w tablicach maturalnych są wzory z których skorzystałam.
21 lis 21:56
Mila:
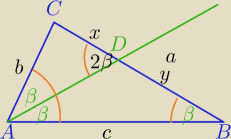
III sposób
10)
AD− dwusieczna kąta A
1) Z tw, o dwusiecznej kąta wewnętrznego
| b | | x | | b | | x | |
| = |
| ⇔ |
| = |
| ⇔b*(a−x)=cx |
| c | | y | | c | | a−x | |
2) ΔADC∼ΔABC:
Podstawiamy do (*)
a
2−b
2=bc
=============
21 lis 22:37
Eta:
IV sposób ( bez sprawdzania i podstawiania do tezy)
| | bc | | ac | | a | |
P(ABC)= |
| sin2β = |
| *sinβ ⇒ cosβ= |
| |
| | 2 | | 2 | | 2b | |
| | a2+c2−b2 | |
z tw. kosinusów cosβ= |
| |
| | 2ac | |
| a2+c2−b2 | | a | |
| = |
| /* 2abc |
| 2ac | | 2b | |
a
2b+c
2b−b
3−a
2c =0 ⇒ a
2(b−c)−b(b−c)(b+c)=0 / : (b−c) , b≠c −−− z treści zadania
a
2−b
2−bc=0
a
2−b
2=bc
c.n.w
21 lis 22:58
Basia: ⇒iteRacj@
ad. 11
nie liczyłam, ale ogólnie to NIE
wielomian (x−5)(x2+x−6) jest podzielny przez x2+x−6, a jego pierwiastki to 5, 2, −3
21 lis 23:08
Mila:
Właśnie miałam też pisać z pola
21 lis 23:09
iteRacj@:
@Basia nie załapałam, co się nie zgadza?
wśród pierwiastków są −3 i 2
21 lis 23:16
Basia: Macies pytał czy to
jedyne pierwiastki
21 lis 23:17
iteRacj@:
zapytał, czy są jednymi (jedne z kilku)
i ja odczytałam, że nie pyta, czy jedynymi
21 lis 23:21
Basia: sorry iteRacja@; chyba już naprawdę niezbyt dobrze widzę; masz rację oczywiście
jeszcze raz przepraszam
21 lis 23:22
iteRacj@:
jednymi z jego pierwiastków są 2 i −3?
dla mnie to znaczyło, że jednymi z wielu i mogą być inne
jak osoby z innych niż moja części Polski piszą tu na forum, to często nie rozumiem
regionalizmów albo zwrotów oczywistych (jest to całkiem fajne)
21 lis 23:24
iteRacj@:
@]P[Basiu]] cieszę się, że mi zwracasz uwagę, jak coś się nie zgadza.
To najlepszy sposób, żeby się skutecznie nauczyć
21 lis 23:27
Eta:
zad 11
Inny sposób niż podają w kluczu
W(x)=2(x−k)(x2+x−6) , gdzie k −−− trzeci pierwiastek
i W(−1)=6 ⇒ −2(1+k)*(−6)=6 ⇒ k= −1/2
to W(x)= (2x+1)(x2+x−6) po wymnożeniu i redukcji
W(x)= 2x3+3x2 −11x −6
a=3, b=−11, c= −6
================
21 lis 23:31
Karol:
21 lis 23:54
Maciess: wyjaśniam, oczywiście chodziło mi o to czy to są pierwiastki tego wielomianu, a nie czy są to
JEDYNE piewiastki
@
Eta Dlaczego od razu zapisałaś postać W(x)=
2(x−k)(x
2+x−6) Ta dwójka przed nawiasem
wynika z oszacowania wyniku dzielenia wielomianu czy jak?
21 lis 23:55
Eta:
Z postaci iloczynowej wielomianu
W(x)=a(x−x1)(x−x2)(x−x3)
a=2
22 lis 00:08