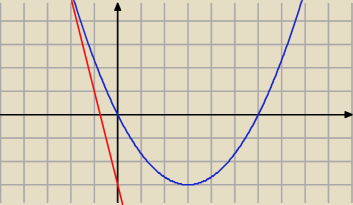
Tangengs funkcji Beata: Córka ma za zadanie w szkole: Wykaż, że g(x)=−4x−3 równa się tangensowi z f(x)=¹₃x²−2x i określ punkt, w którym się spotykają. Jako, że matematykę miałam 20 lat temu, nie mam kompletnego pojęcia jak jej pomóc

6latek:

ABC: W jakiej córka jest szkole? strasznie dziwne to polecenie

Mila: Coś ta treść źle napisana, sprawdź i popraw, najlepiej , aby córka tu się pojawiła i zadała pytania.

o kurde: co to jest tg z funkcji funkcja tryognometryczna z paraboli ... ze jak ?o co kaman

Beata: Niemieckie gimnazjum, mogła zapisać błędnie "równa się tangensowi z" zamiast "jest tangensem z". Córka niestety nie mówi po polsku.

o kurde:

ABC: hmmm ... w niemieckim gimnazjum chyba rachunku różniczkowego nie mają?

Beata: Mają rachunek różniczkowy

6latek: A teraz spojrz w lustro o zobacz czy nie upodabniasz sie do naszego premiera Zobacz czy Twoj nos sie nie wydluza

ABC: ale jaja ! dzieci 13 letnie?

Beata: Gimnazjum w sensie ich szkołę średnią, czyli gymnasium, 17 lat ma, nie 13.

Adamm: treść jest błędna tak czy siak, i nie chodzi tu o gramatykę

PW:

	1
−4x−3=		x2−2x
	3

−12x−9=x²−6x 0=x²+6x+9 0=(x+3)² − równanie to ma jedno rozwiązanie, Pewnie idzie o punkt wspólny prostej i paraboli (punkt styczności?)

Beata: Tak, punkt styczności

o kurde: a co z tym tangensem ?

Adamm: chodziło pewnie o to że g jest styczną do f, i trzeba to sprawdzić

Mila: 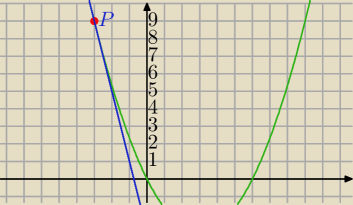Beato Zobacz podobne zadanie w podręczniku, albo w zeszycie. Może coś wymyślimy, bo jest bez sensu. g(x)=−4x−3

	1
f(x)=		x2−2x
	3

Może chodzi styczną w punkcie przecięcia?

	1
−4x−3=		x2−2x
	3

1
	x2+2x+3=0 /*3
3

x²+6x+9=0 (x+3)²=0 x=−3 y=−4*(−3)−3=9 P=(−3,9) Styczna : w p.(−3,9) y=f'(−3)*(x+3)+f(−3)

	1
f'(x)=		*2x−2
	3

	1
f'(−3)=		*2*(−3)−2=−4
	3

Styczna : y=−4(x+3)+9 y=−4x−12+9 y=−4x−3 tgα=−4

o kurde: nadal nie wiem co ma do tego tangens.

Mila: Prosta y=−4x−3 jest styczną do paraboli w p. P=(−3,9)

o kurde: no teraz kapuje

o kurde: rany Julek, po tresci polecenia mialem totalny metlik

Beata: Mila, wydaję mi się, że dokładnie o to chodziło, dziękuję bardzo!

PW: Jeżeli to jest gimnazjum, ro mogli przyjąć definicję stycznej do paraboli jako takiej prostej, która nie jest pionowa i ma z parabolą dokładnie jeden punkt wspólny. Wtedy nie jest potrzebna pochodna.

Beata: Gimnazjum w Niemczech jest zakończone maturą, jak polskie liceum.

PW: A my tyle z germanizacją walczyli Jeżeli córka miała już pojęcie pochodnej i stycznej do wykresu opowiedzianej w języku pochodnych, to rozwiązanie Mili jest kompletne.

Blee: PW −−− Beata nie mieszka w Polsce tylko (zapewne USA), więc: 1) inny program, 2) gimnazjum ≠ gimnazjum w Polsce (chodzi o samo określenie poziomu nauczania)

Mila: A moją mamę chciał Niemiec zastrzelić za wałówkę dla powstańców, a drugi Niemiec mądry nie zgodził się. ( Nordycki wygląd miała )

ABC: takie życie... u mnie jeden dziadek przeżył obóz w Dachau a drugi uciekł Rosjanom z transportu do Starobielska..o mało co bym się nie urodził

PW: He, he, niemal identyczne zdarzenie miała moja mama (wyszła z domu po godzinie policyjnej). Moja starsza siostra uwieczniła to w książce.

Beata: Córka twierdzi, że wygląda dobrze, więc dziękuję raz jeszcze za pomoc! ☺️

Mariusz: Jeden punkt masz ustalony Rysujesz sieczne do wykresu funkcji f(x) Proste przechodzące przez dwa punkty wspólne z wykresem funkcji f(x) przy czym ten drugi punkt siecznej wspólny z wykresem funkcji f(x) zbliża się do tego ustalonego punktu (odległość między punktami wspólnymi z wykresem funkcji f(x) jest coraz mniejsza) Współczynniki kierunkowe tych siecznych tworzą ciąg którego granica to współczynnik kierunkowy stycznej Teraz trzeba objaśnić co to jest ciąg oraz granica Ciąg jest to funkcja z N do R ∀_ε>0∃_δ>0∀_x∊D 0<|x−x₀|<δ ⇒ |f(x) − g| < ε Może chodziło o to że z jednej strony współczynnik kierunkowy prostej to tangens nachylenia prostej do osi OX a z drugiej strony współczynnik kierunkowy stycznej to pochodna funkcji w punkcie tylko czy aby na pewno takie zadania byłyby w gimnazjum

Mariusz: ABC , skąd wiesz że jej córka jest w Niemczech Jak tak to tam mają inne gimnazjum

ABC: prześledź wątek od początku powoli

Mariusz: A już widzę, wpis z 21 lis 2018 18:37 Jakoś musiałem go ominąć Może błędna treść zadania wynika z błędnego przekładu z języka niemieckiego Jak tak to Mila rozwiązała to zadanie ABC , kiedyś dałem dwa ciągi aby zgadli ich wyraz ogólny i mi zaspamowali temat Jeden był związany z tabelą rozmiarów obuwia a drugi z tabelą z kalendarzem Dałem też funkcje która miała czytać/pisać do pliku ale znalazł się taki który tylko udawał że umie programować i znowu zaspamował mi temat więc jak widzisz rzadko zdarza się że ktoś sensownie odpowie jak tutaj Mila