próbna matura Operon arkusz podstawowy ite: dla zainteresowanych dzisiejszą próbną maturą, arkusz podstawowy http://arkusze.gieldamaturalna.pl/uploads/dfb9d32e5dd6aeba9e804b0bd9a36e09823d4080.pdf

fsdgses: jak zwykle banalne zadania

6latek: Mysle ze w zadaniu nr 11 jest blad Podstawa funkcji ma wartosc ujemna a powinnaa byc >0

fsdgses: podstawa jest 3 wiec o co ci chodzi?

Jerzy: Cześć Byłby błąd, gdyby było: f(x) = (−3)^x

6latek: Dzien dobry Jerzy Takie zapisy sa dla mnie niejednoznaczne jak bym to mial przeksztalcic zeby posdatwa byla >0? Kolego jesli juz odpowiadasz to nalezy napisac dlaczego Odpowiedz w stylu nie bo nie czy tak bo tak jest imfaltymna

Jerzy: Nie żartuj −2² = −4 , ale (−2)² = 4 Zapis jest jednoznaczny: f(x) = −3^x , czyli f(x) = − g(x) , gdzie: g(x) = 3^x

Adamm: zd 27 (a+b/2)²−(a−b/2)² = 2ab 4|(2ab) bo 2|a lub 2|b, z racji tego że to są 2 kolejne liczby naturalne

6latek: Dobrze . pozniej sie odezwe

Adamm: reszta zadań dosyć nudna

Basia: Jak zwykle na poziomie podstawowym Adammie Witajcie

Maciess: A co powiecie na to, że trapez którego boki liczymy nie powinien istnieć?

Mila: Dla 6latka. zad 11. Zapis : f(x)=−3^x=(−1)*3^x f(x−2)=(−1)*3^x−2=−3^x−2

Mila: 31)

ite: @Maciess chodzi o ΔAPB w zad.26 (o trapezie)? z danych: |AP|=8, |BP|=12, z odpowiedzi: |AB| = 24

Maciess: Mógłby ktoś rozwiązać 33?

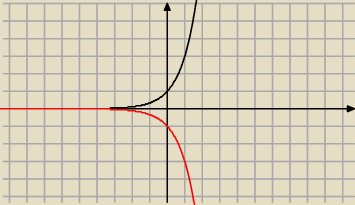
6latek: Dobry wieczor Milu tak .Juz to rozumiem

ite: podobny problem z ΔDCP

Maciess: @ite

	9
chodzi o ΔDCP. Boki (nawet wg klucza) to 3,9,
	2

Maciek: Matura jak matura, sam pisałem , będę miał ~86% ale nie przywiązuje zbyt dużej wagi do niej

fsdgses: co tak słabo?

Blee: Maciess co do zadania 33 1) wniosek z treści zadania: wierzchołek B to punkt przecięcia się tych dwóch prostych ... stąd: B ma współrzędne (15,8)

	2
2) AC prostopadła do wysokości z B ... więc AC leży na prostej y =		x + b
	3

3) wyznaczamy 'b' podstawiając współrzędne punktu A: 8 = −6 + b −> b= 2 4) punkt C leży na przecięciu się prostych: y = −2x + 38

	2
y =		x + 2
	3

więc ma współrzędne (13.5 ; 11) 5) wyznaczamy prostą zawierającą AB (podstawiamy współrzędne punktów ..... (tego już mi się nie chce robić ) 6) robimy prostopadłą do wyznaczonej prostej i wyznaczamy 'wyraz wolny' tak aby ta prosta przechodziła przez wierzchołek C Koooniec

Maciess: Dziękuje Blee, jutro sobie to policze na swojej karteczce zobacze czy wyjdzie.