proszę o rozwiązanie Anna:

	2
na gałęzi hiperboli o równaniu y =		gdzie x ∊ ( − ∞ .0 ) wyznacz taki punkt P którego
	x

odległość od punktu A(1, −1) jest najmniejsza

	2		2
P ( x;		) ∊ y =
	x		x

	2		4		4
IAP I = √(x−1)2 +(		+1)2 = √x2 − 2x +1 +		+		+1
	x		x2		x

po obliczeniu pochodnej

	4		4		8x		4
( √x2 − 2x +1 +		+		+1), = 2x − 2 −		−
	x2		x		x4		x2

	8x		4
2x − 2 −		−		=0
	x4		x2

dalej nie wiem

ABC: w ten sposób zaliczysz się na śmierć, wykorzystaj fakt że odległość jako funkcja nieujemna osiąga ekstremum wtedy i tylko wtedy gdy jej kwadrat osiąga ekstremum

Anna: nie wiem jak to wykonać proszę o rozwiązanie

ABC: zamiast tego co oznaczyłaś IAP I badaj IAP I² łatwiejsza będzie pochodna do obliczenia.

Anna: ja i tak liczyłam pochodną tylko z wyrażenia pod pierwiastkiem

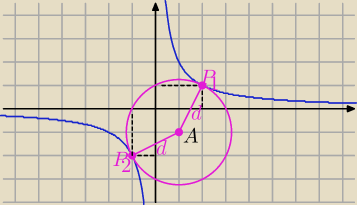
Eta: Proponuję tak:

	2
y=		, A(1,−1)
	x

	−2		x2
y'=		to prosta prostopadła ma współczynnik
	x2		2

piszę jej równanie

	x2		2
y=		(x−1)−1 i y=		( rozwiązuję układ równań
	2		x

	x3		x2		2
		−		−1=		/*2x
	2		2		x

x⁴−x³−2x−4=0 W(−1)= 1+1+1−4=0 ⇒ x= −1 po rozkładzie na czynniki : (x+1)(x−2)(x²+2)=0 ⇒ x=−1 v x= 2

	2		2
to y=		=−2 v y=		=1
	−1		2

I mamy dwa takie punkty na hiperboli których odległość od A jest najmniejsza P(−1,−2) , P(1,2) =============

Eta:

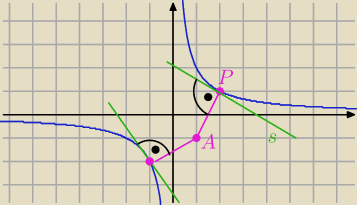
	2
Dla jasności współczynnik kierunkowy stycznej s a= −
	x2

	x2
współczynnik kierunkowy prostej AP ⊥s a=
	2

Anna: dziękuję bardzo

janek191: P = ( − 1, − 2) lub P = ( 2,1)