Badanie funkcji UczącySię: Cześć, dostałem zadanie aby zbadać funkcję f(x) = px{x} (pierwiastek st. x z x No to: Dziedzina : x > 0 Zbiór wartości: y ∊[0 , ∞ ) Nie umiem tej funkcji narysować, znajduję tylko kilka punktów

	1		1−x2
f'(x) =		* x{		}
	x		x

I nie wiem co dalej. Proszę o wskazówki... tzn. wiem że teraz chodzi o ekstrema ale nie wiem jak je policzyć tutaj

ABC: zbiór wartości nie może być taki jak piszesz bo lim_n→∞ⁿ√n=1 pochodna też nie taka naprawdę jest jak u ciebie

ABC: z tego co pamiętam to dla x=e wartość tej funkcji e^1/e jest ekstremalna

UczącySię: Co do zbioru wartości się zgodzę, ale z pochodną niezbyt, ponieważ

	1
f'(x) = x1/x' =		* x1/x −1.
	x

A jakieś wskazówki co zrobić jak mam pochodną

ABC: ten wzór na pochodną który ty podajesz obowiązuje przy ustalonym wykładniku ! zauważ że tu jednocześnie się zmienia podstawa potęgi jak również wykładnik

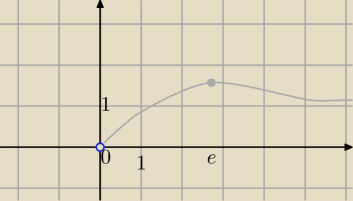
Mila: f(x)=x^1/x, f(x)>0, x>0 pochodna funkcji: y=x⁽1/x)

	lnx
y'=(x1/x)'=(elnx1/x)'=(elnxx)'=elnxx*(		)'
	x

	1x*x−lnx		1−lnx
y'=x1x*		=x1x*
	x2		x2

y'=x^1_x−2*(1−lnx) y'>0 ⇔1−lnx>0⇔1>lnx⇔x∊(0,e) funkcja rosnąca, dla x>e funkcja jest malejąca dla x=e funkcja f(x) ma maksimum f(e)=e^1/e e≈2,7 oblicz przybliżoną wartość około 1,5 Lim _x→∞x^1/x=1 Może ICSP spojrzy i coś doda

UczącySię: Ja nigdy nie rozumiem dlaczego zawsze w dziwnych miejscach pojawia się ta znienawidzona przeze mnie liczba Eulera ... Milu, możesz mi wytłumaczyć skąd da pochodna, a dokładniej druga równość w jej liczeniu

ABC: jak ktoś jeszcze rozpisze punkt przegięcia to się zdziwię , tam chyba trzeba by z równaniem przestępnym się uporać

UczącySię: Ja najpierw chciałbym ogarnąć to co tutaj, owy punkt do dla mnie na razie "przegięcie" hehe

UczącySię: Milu, a czemu przy liczeniu pochodnej z e^lnx1/x 'x' wskoczył jako mianownik do logarytmu I drugie pytanie, czy konieczne jest aby zamienić to na e^lnx ? Bo można także inne, co nam to 'e' daje ?

Mila: 1) Masz w innej postaci zapisaną funkcję, Korzystasz z własności (e^x)'=e^x i własności funkcji wykładniczej: e^ln(5)=5 e^lnx=x e^ln1000=1000 2^log₂(7)=7 To na pewno znasz doskonale.

	1		lnx
2) lnx1/x=		*lnx=
	x		x

stąd :

	1		lnx
(lnx1/x)'=(		*lnx)'=(		)'
	x		x

3) Euler to był geniusz i nie narzekaj na liczbe e, ma wiele zalet

Mila: Nie jest konieczne korzystać z tej zamiany, ale ułatwia liczenie w tym przypadku .

ABC: x^y=e^y*ln(x) to jest standardowy sposób potęgowania w wyższej matematyce, przyda ci się jak będziesz chciał potęgować liczby ujemne na przykład (−1,5)^0,237 tak możesz policzyć wynik będzie liczbą zespoloną,więc się przyzwyczajaj do niego jak najwcześniej

UczącySię: Ehhh Milu, no przecież, i to takie działania już w liceum były .... no to źle ze mną. 1) oczywiście znam Do Eulera nic nie mam, tylko nie do końca rozumiem Jego liczbę

Mila: Powodzenia w dalszych zmaganiach z królową nauk: Dobranoc

ABC: e^iπ+1=0 mój kolega mówił że może na to równanie patrzeć godzinami − cały świat jest w nim zawarty

UczącySię: Milu raz jeszcze Ci dziękuję za pomoc ! ABC Tobie również dzięki Lepiej oddać się poezji

poezja: zostań przy matematyce

UczącySię: Tylko ja niestety dalej nie rozumiem liczenia pierwszej pochodnej ... po co w ogóle ten logarytm

Jerzy: To jest metoda liczenia pochodnej funkcji złożonej typu: [f(x)]^g(x). Wykorzystuje sie własność: e^lna = a Np: h(x) = x^x = e^lnxx = e^x*lnx