Równanie pheri: Zadanie: Dla jakich wartości m równanie |x²−2x−1|=m ma dokładnie 3 rozwiązania? Jak to rozwiązać sposobem algebraicznym? Proszę o pomoc lub wskazówkę

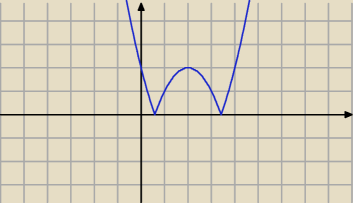
Blee: 1) szukasz wierzchołka paraboli f(x) = x²−2x−1 2) nakładasz moduł na funkcję 3) |f(x_wierzchołka| <−−− dla takiego m będą trzy rozwiązania Rysunek przedstawia przykładową funkcję kwadratową na którą nałożono moduł

pheri: Blee, dziękuje!

Mila: f(x)=|x²−2x−1|=|(x−1)²−2| x_w=1, y_w=−2 −współrzędne wierzchołka paraboli y=x²−2x−1 parabola skierowana ramionami do góry Dla m>−2 są dwa rozwiązania równania x²−2x−1=m Zatem: |f(1)|=|−2|=2 dla m=2 −trzy rozwiązania równania |f(x)|=m