rozwiązać nierówność zadanie: hej mam rozwiązać nierówność: |x² −5x+6| + |x²−4|<bądź równe −(x−2)² i teraz pierwszy nawias z delty wyliczam i wychodzi: |(x+3)(x+2)| + |(x−2)(x+2)| < bądz równe −(x−2)² I teraz chciała się upewnić, że x spradzam dla przedziałów takich : 1) (−nieskończoność, −3) 2)<−3 , −2) 3) <−2, 2) 4) <2, +nieskończonść) tak?

ABC: po lewej stronie masz sumę dwóch wyrażeń nieujemnych, więc jest ona nieujemna po prawej stronie masz wyrażenie niedodatnie twoja nierówność mogłaby zachodzić tylko gdyby był taki x, dla którego obie strony się zerują

zadanie: A to błędne jest rozpisanie przedziałów na te powyższe, bo one się wzięły właśnie z x, które zerują nawiasy

ABC: nie musisz nic dzielić na przedziały prawa strona zeruje się tylko gdy x=2 lewa strona zeruje się gdy x²−5x+6=0 i jednocześnie x²−4=0 pierwsze z nich się zeruje gdy x=2 lub x=3 drugie gdy x=−2 lub x=2 oba jednocześnie zerują się tylko dla x=2 rozwiązaniem twojej nierówności jest zbiór jednoelementowy

zadanie: aaaa tak łatwo można było, dziękuję bardzo!

zadanie: A mam jeszcze pytanie upewniające. mam rozwiązać nierówność: |x²−6x+7| <lub równe x²−1 i teraz analogicznie moduł zeruje się wyliczając z delty dla x= 3 +√2 lub x=3−√2 Prawa strona zeruje się dla x=1 lub x=−1 czyli odpowiedzią będzie x = pusty zbiór, bo pierwiastki lewej i prawej strony się nie pokrywają ?

ABC: tu niestety nie ma tak dobrze, w tamtym zadaniu tak było z uwagi na szczególną postać wyrażenia −(x−2)² tutaj już raczej trzeba rozważać przypadki

ICSP: |x² − 6x + 7| < x² − 1 Dla |x| ≤ 1 nierówność jest sprzeczna. Dla pozostałych mamy (−6x + 8)(2x² − 6x + 6) < 0 6x ≥ 8

	4
x ≥
	3

ICSP:

	4
x >
	3

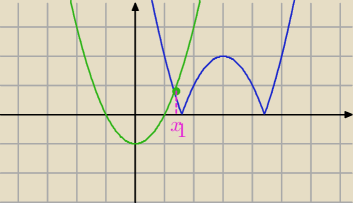
Mila: Metoda graficzna : f(x)=|x²−6x+7| g(x)=x²−1 f(x)≤g(x) wykres niebieski leży poniżej wykresu zielonego dla x≥x₁ x²−6x+7=x²−1 −6x=−8

	4
x=
	3

	4
x≥
	3

zadanie: rozumiem, następnym razem wybiore metodę graficzną, bo z rozpisywaniem przedziałów można się pogubić dziękuję

Mila: