wielokaty na plaszczynie wielokat: W okrąg wpisano prostokąt. Jaką maksymalną część koła może zajmować ten prostokąt?

Blee: przekątna prostokąta ma stałą długość i wynosi ona 2R więc a² + b² = 4R² −> a = √4R² − b² P = a*b = b*√4R² − b² pochodna ... i liczysz

Tadeusz: ... i przekonasz się, że ten prostokąt to kwadrat

PW: Można też: Przekątne prostokąta połowią się i mają jednakowe długości. Niech te połówki mają długość x, a kąty między nimi niech mają miary α i π−α (α≤π−α), przy czym dla prostokąta wpisanego w koło liczba x jest stała, równa promieniowi koła. Jego pole jest równe Pole prostokąta jest równe

	π
x2sinα + x2sin(π−α) =x2sinα+x2sinα = 2x2sinα, α∊(0,		>.
	2

	π		π
Funkcja sinus na przedziale (0,		> osiaga maksimum dla α=		.
	2		2

	π
Odpowiedź: Prostokąt ma maksymalne pole, gdy α=		, to znaczy gdy jest kwadratem.
	2

Maksymalne pole jest równe

	π
2r2sin		= 2r2•1 = 2r2
	2

Stosunek pola kwadratu do pola koła jest równy

	2r2		2
		=		.
	πr2		π

Blee: Tadeusz ... czemu zdradzasz zakończenie Ładnie to tak

PW: Oj, wszystko zepsułem…

Mila:

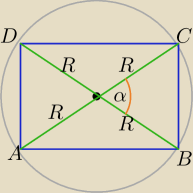
	2R*2R
PABCD=		*sinα=2R2*sinα
	2

Największe pole dla α=90^o⇔ ABCD jest kwadratem .

2R2		2
	=
πR2		π

wielokat: Dziękuję wszystkim za pomoc!