wielokąty na płaszczyźnie wielokątnapłaszczyźnie: Przy jakiej długości wysokości trójkąt równoramienny wpisany w okrąg o promieniu R ma największe pole?

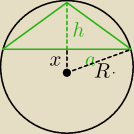
Jerzy: x + h = R ⇔ h = R − x x² + a² = R² ⇔ a = √R² − x²

	1
P =		2ah = ah
	2

P = (R − x)√R² − x²

wielokątnapłaszczyźnie: Co nam to daje?

Jerzy: Daje nam funkcję i trzeba znaleźć jej maksimum.

wielokątnapłaszczyźnie: Zakładając, że R jest stałą?

Jerzy: Tak,R to stała.

wielokątnapłaszczyźnie: Ok, już rozumiem. Dziękuję.

wielokątnapłaszczyźnie: Wyszła mi pochodna g'(x)=−4x³+6Rx²−2R³. Czy to możliwe?

Jerzy: Raczej nie. W pochodnej musi być pierwiastek.Skąd w pochodnej R³ ?

Jerzy: Skorzystaj ze wzoru na pochodną iloczynu.

wielokatnaplaszczyznie: "Wciagnelam" R−x pod pierwiastek. Wyrazenie osiagnie wartosc najwieksza, gdy wyrazenie pod pierwiastkiem bedzie najwieksze. Wowczas analizuje tylko to, co pod pierwiastkiem i z tego licze pochodna.

Jerzy:

	x(R − x)
P'(x) = −√...... −
	√.....

wielokątnapłaszczyźnie: Dlaczego nie mogę zrobić, że: P(x)=√R²−x²*(R−x)=√(R²−x²)*(R−x)²=√−x⁴+2Rx³−2R³x+R⁴. To osiąga wartość największą, gdy −x⁴+2Rx³−2R³x+R⁴ będzie największe. Zatem liczę pochodną g(x)=−x⁴+2Rx³−2R³x+R⁴, czyli g'(x)=−4x³+6Rx²−2R³ ?

wielokątnapłaszczyźnie: ?

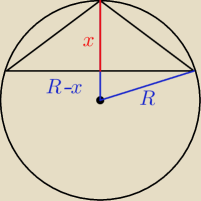
an: Zadanie dla jakiej wysokośći ...

Jerzy: Zawsze od R można odjąć optymalne x i otrzmać optymalne h.

an:

	3
P=x√2Rx−x2 ⇒P'⇒xmax=		R
	2

a u Ciebie x =1 i co dalej

Jerzy: Popatrz uważniej na "moje" P (10:57).