Liczby zespolone simon5005: Zaznacz na płaszczyźnie zbiór punktów odpowiadającym liczbom zespolonym spełniającym warunki: |z−1| + |z + 1| = 3 Wiem to, że ma powstać tutaj elipsa, tylko nie bardzo rozumiem skąd się bierze potem do tego takie równanie:

	3
y2 + 1 = (		)2
	2

ABC: suma odległości od dwóch punktów ognisk( 1, −1) jest stała (równa 3) więc to jest elipsa gdy podstawisz z=x+yi i przekształcisz powinno ci wyjść ale chyba nie zupełnie tak jak napisałeś

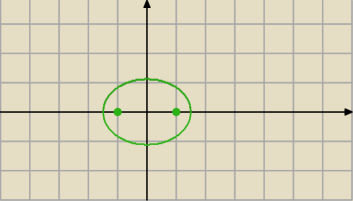
Mila: Poczytaj o elipsie.

x2		y2
	+		=1
a2		b2

Ogniska : (1,0),(−1,0) odległość między nimi: 2c=2 c=1 2a=3

	3
a=		− półoś
	2

Wzór : c²=a²−b²

	3
1=(		)2−b2
	2

	5
b2=
	4

	√5
b=
	2

x2		y2
	+		=1
(3/2)2		(√5/2)2

II sposób z=x+iy |x+iy−1|+|x+iy+1|=3 √(x−1)²+y²+√(x+1)²+y²=3 √(x+1)²+y²=3 −√(x−1)²+y²/² x²+2x+1+y²=9−6√(x−1)²+y²+x²−2x+1+y² 4x=9−6√x²−2x+1+y² 4x−9=−6√x²−2x+1+y² 9−4x=6√x²−2x+1+y²/² 81−72x+16x²=36(x²−2x+1+y²) 81−72x+16x²=36x²−72x+36+36y² 20x²+36y²=45 /:45

20x2		36y2
	+		=1
45		45

x2		y2
	+		=1
(9/4)		5/4

simon5005: Dziękuję serdecznie za te dwa sposoby rozwiązania. Teraz już wszystko jest jasne. Pozdrawiam

Mila: