Układ nierówności z wartością bezwzględną, ilość rozwiązań układu równań.
Wojciech: Witam!
To moje pierwsze pytanie tutaj, ale proszę o pomoc, bo urywam sobie głowę, jak to zrobić
Układ nierówności − Przedstaw ilustrację graficzną układu:
|x−y|≥6
|y|≤|x|
Dostałem również ten sam układ ze strzałkami w drugą stronę, ale sądzę, że jego wykonanie
będzie podobne.
Zad. 2
Zbadaj liczbę rozwiązań równania w zależności od parametru a (układ równań)
ax − 3ay = 3
x + ay = a − 2
Korzystam z metody wyznaczników.
Wychodzi mi przypadek dla układu oznaczonego (a!=0 a!=3), później rozpatruję drugi przypadek
− układ nieoznaczony,
gdzie wychodzi mi a = 3, ale kiedy biorę trzeci przypadek − czyli układ sprzeczny − nie
wychodzi mi (prawdopodobnie źle interpretuję zdanie logiczne)
(a = 3 V a = −3) [(a!=0 a!=3) V (a!=−1 a!=3)]
Kiedy do wyznaczników podstawiam zero wychodzi układ sprzeczny bez żadnych problemów.
Pozdrawiam
17 lis 20:36
iteRacj@:
2/ wyznacznik główny układu
|a −3a|
|1 a| =a2−(−3a)*1=a2+3a=a(a+3)
więc przypadek dla układu oznaczonego a=0 ∨ a=−3
17 lis 20:56
iteRacj@: * oczywiście a≠0 ∨ a≠−3
17 lis 20:59
Wojciech: Wybaczcie za błąd, pierwsze równanie powinno wyglądać tak: ax + 3ay = 3
17 lis 21:06
iteRacj@:
W=a(a−3)
Wx=−3a(a−3)
Wy=(a+1)(a−3)
układ oznaczony dla a≠0 ∧ a≠3 (W≠0)
układ sprzeczny dla a=0 (W=0 i Wx=0 i Wy≠0)
układ nieoznaczony dla a=3 (W=0 i Wx=0 i Wy=0)
17 lis 21:20
Wojciech: Dzięki, a byłbyś w stanie wyjaśnić, dlaczego z tego zdania logicznego, które zapisałem, nie
wychodzi?
17 lis 21:27
6latek: A niby jakie logiczne zdanie ?
logicznie to nalezy pomyslec i spojrzec na warunki jakie musi spelniac aby byl ukladem np
sprzecznym
17 lis 21:35
iteRacj@:
1/ zaczynam od pytania: dla jakich wartości a będzie spełniony warunek W≠0
2/ skoro odpowiedzią jest a≠0 ∧ a≠3, to wiem już kiedy układ będzie oznaczony
3/ potem zastanawiam się, jaki będzie układ czyli jakie wartości przyjmą Wx i Wy dla tych
odrzuconych wartości a=0 oraz dla a=3
4/ podstawiam najpierw jedną potem drugą wartość i akurat tutaj otrzymuję raz (W=0 i Wx=0 i
Wy≠0) a drugi (W=0 i Wx=0 i Wy=0)
Ty sprawdzasz warunki od końca czyli od pytania, kiedy zerują się Wx i Wy. I znajdujesz
wartości a, a potem sprawdasz dla nich wartość W. To dłuższa droga i łatwiej o pomyłkę.
17 lis 21:44
6latek:

To jest ilustracja graficzna nierownosci |x−y|≥6
Dorysuj teraz |y|≤|x|
Mysle ze nalezy rozpatrzyc przypadki
1) y≥0 i x≥0
y≤x
2) y≥0 i x<0
y≤−x
3) y<0 x≥0
−y≤x y≥−x
4) y<0 i x<0
−y≤−x y≥x
17 lis 21:55
Wojciech: Dobra, teraz zadziałało, dzięki.
17 lis 21:55
Wojciech: Rozpatrzę, w jaki sposób tą pierwszą nierówność narysować?
17 lis 21:56
6latek:
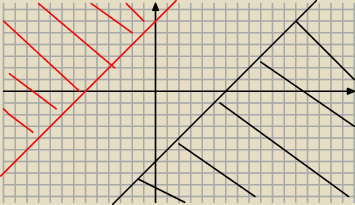
Nierownosc |x|≥y jest rownowazna alternatywie nierownosci
x≥y lub x≤−y
wiec |x−y|≥6 jest rownowazna alternatywie nierownosci
x−y≥6 to y≤x−6
lub x−y≤−6 to y≥6+x i rysujesz sume rozwiazan
To jest wlasnie rozwiazanie tej nierownosci wraz z liniami .
17 lis 22:05
6latek: mam nadzieje ze nie namacilem z ta druga nierownoscia
17 lis 22:09
iteRacj@:
jeszcze co do pytania z 21:27
W=a(a−3)
Wx=−3a(a−3)
Wy=(a+1)(a−3)
kiedy układ będzie sprzeczny?
W=0 ∧ (Wx≠0 ∨ Wy≠0) ⇔ (W=0 ∧ Wx≠0) ∨ (W=0 ∧ Wy≠0)
czyli (a=0 ∨ a−3=0) ∧ ((−3a≠0 ∧ a−3≠0) ∨ (a+1≠0 ∧ a−3≠0))
17 lis 22:12
iteRacj@:
@ 6latku otwórz geogebrę i po prostu wklej obie nierówności, sprawdzisz, czy prawidłowo
rysujesz
17 lis 22:18
6latek: Dobry wieczor

Chyba juz widze .
17 lis 22:32
17 lis 22:33
17 lis 22:46
17 lis 22:54
Wojciech: Dzięki Panowie, myślałem, że to z nierównościami trudniejsze

18 lis 09:49
18 lis 10:05
 To jest ilustracja graficzna nierownosci |x−y|≥6
Dorysuj teraz |y|≤|x|
Mysle ze nalezy rozpatrzyc przypadki
1) y≥0 i x≥0
y≤x
2) y≥0 i x<0
y≤−x
3) y<0 x≥0
−y≤x y≥−x
4) y<0 i x<0
−y≤−x y≥x
To jest ilustracja graficzna nierownosci |x−y|≥6
Dorysuj teraz |y|≤|x|
Mysle ze nalezy rozpatrzyc przypadki
1) y≥0 i x≥0
y≤x
2) y≥0 i x<0
y≤−x
3) y<0 x≥0
−y≤x y≥−x
4) y<0 i x<0
−y≤−x y≥x
 Nierownosc |x|≥y jest rownowazna alternatywie nierownosci
x≥y lub x≤−y
wiec |x−y|≥6 jest rownowazna alternatywie nierownosci
x−y≥6 to y≤x−6
lub x−y≤−6 to y≥6+x i rysujesz sume rozwiazan
To jest wlasnie rozwiazanie tej nierownosci wraz z liniami .
Nierownosc |x|≥y jest rownowazna alternatywie nierownosci
x≥y lub x≤−y
wiec |x−y|≥6 jest rownowazna alternatywie nierownosci
x−y≥6 to y≤x−6
lub x−y≤−6 to y≥6+x i rysujesz sume rozwiazan
To jest wlasnie rozwiazanie tej nierownosci wraz z liniami .
 Chyba juz widze .
Chyba juz widze .

 Posluchaj tego . Lubie bardzo jak spiewa . Spiewczka rockowa z glosem operowym
https://www.youtube.com/watch?v=GAAXuLt1Ffg
Posluchaj tego . Lubie bardzo jak spiewa . Spiewczka rockowa z glosem operowym
https://www.youtube.com/watch?v=GAAXuLt1Ffg
