Metryka Ola: Q(x,y)= 3|x1−y1| + 1/2|x2−y2| jest metryką w R² wiem, że postać kul otwartych ma mieć postać x2=6x1 i x2=−6x1 Wiem, że to wynika ze stosunku 3/ (1/2) = 6, ale dlaczego to ma mieć postac x2=6x1 i x2=−6x1 ? Ktoś potrafi mi to ładnie rozpisac i wyhaśnić o co chodzi?

Ola: Ktoś cos?

Ola: Ktoś cos?

jc: |x−y| jest metryką na prostej. Wykorzystaj ten fakt.

Ola: Nie rozumiem w ogole czemu tak jest. Nikt nam na wykładzie tego nie wytlumaczył Możesz krok po kroku to rozpisac ?

Ola: Nie rozumiem w ogole czemu tak jest. Nikt nam na wykładzie tego nie wytlumaczył Możesz krok po kroku to rozpisac ?

jc: |x−y|≥0, |x−y|=0 ⇔x=y |x−y|=|y−x| |a+b|≤|a|+|b| podstawiasz a=x−y, b=y−z i masz |x−z| ≤ |x−y| +|y−z| Teraz masz Q[(x,x'), (y,y')] = 3|x−y| + (1/2) |x'−y'|. Każda z 3 własności jest teraz łatwa do sprawdzenia, n.p. Q[(x,x'), (y,y')] = 3|x−y| + (1/2) |x'−y'| = = 3|y−x| + (1/2) |y'−x'| = Q[(y,y'), (x,x')] Aby nie pisać indeksów, użyłem nieco innych oznaczeń.

Ola: Ja rozumiem wszystkie te własności i wiem co napisałeś , ale nie wiem jak przejść do postaci x2 = 6x1 i x2=−6x1. Często też piszą, ze kula jest kwadratem czy tam rombem , a ja kompletnie nie wiem dlaczego. Nie mam pojęcia co Twoj zapis wnosi do mojego pytania.

jc: Jeśli bardzo chcesz pisać indeksy, to spójrz na podpowiedź po lewej stronie. Zawsze warto czytelnie zapisywać wzory, matematyka i bez tego nie jest łatwa. Wydaje mi się, że bez indeksów zapis jest czytelniejszy. Pokazałem, że wszystko sprowadza się do przypadku jednowymiarowego. Ogólnie, jeśli masz dwie metryki d₁ i d₂ i dwie dodatnie liczby a₁, a₂, to d((x₁, x₂), (y₁,y₂)) = a₁ d₁(x₁,y₁) + a₂ d₂(x₂,y₂) jest metryką na iloczynie kartezjańskim.

Ola: Tłumaczysz to strasznie po akademicku i chyba nie wiesz o co mi chodzi. Serio ,ja próbuję to zrozumieć i głowię się już nad tym godzinę jak to doprowadzić do postaci jaka jest w odpowiedzi, ale po prostu nie kminię w ogóle tych pojęć, bo nam koleś tego dobrz enie wytłuamczył A Twoje tłumaczenia są mniej więcej takie jakbyś dziecku z podstawówki tłumaczył zadania z matury rozszerzonej. Jak już wspomniałam , rozumiem cąły Twój zapisa, ale nie wiem co to ma do mojego pytania jak to doprowadzić do wyżej wymienionej postaci.

jc: Oj, chyba rozumiem. Masz narysować kulę w zadanej metryce. Narysuj kulę o środku (0,0), przesunięta kula będzie wyglądała tak samo. 3 |x| + |y|/2 ≤ r Uważaj, bo znów zmieniłem oznaczenia. Patrzysz na pierwszą ćwiartkę. Obraz w pozostałych uzyskujesz odbijając symetrycznie rysunek w pierwszej ćwiartce. Brzeg koła w pierwszej ćwiartce, to linia 3x+y/2=r Linia ta przecina oś x−ów w punkcie x=r/3, a oś y−ów w punkcie y=2. 3|x−x₀| + |y−y₀|/2 ≤ r to nasza poprzednia kula, czyli romb, przesunięta o wektor (x₀, y₀).

jc: Popraw, zamiast y=2, powinno być y=2r.

Ola: a jak doprowadzic w dalszym ciągu do nierownosci x2 = 6x1 i x2 = −6x1? Tutaj mam zadanie o ktore pytam 2.40 : http://math.uni.lodz.pl/~wiertelak/zbior.pdf Autor po króte coś wytłumaczył, ale ja nie rozumiem tego zapisu

Ola: Dowiodłam już, że to jest metryką na zbiorze R^[2}

Ola: w tym linku też są odpowiedzi. Moze to Cię naprowadzi o co mi chodzi. Kompletnie nie wiem o co autoriowi hchodzi w tym zapisie

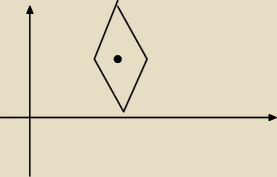
jc: Ola, teraz pisałbym tak: Q[(x,y), (a,b)] = 3|x−a| +|y−b|/2. Porównaj to ze wzorem d[(x,y),(a,b)]=√(x−a)²+(y−b)² Nierówność √(x−a)²+(y−b)² ≤ r opisuje zwykłą kulę o środku w punkcie (a,b) i promieniu r. Twoja kula opisana jest nierównością: 3|x−a| +|y−b|/2 ≤ r. Na rysunku ma być romb o wierzchołkach (góra, dół, prawy, lewy) (a+r/3,b),(a−r/3,b), (a,b+2r), (a,b−2b)

Ola: Jeśli jesteś przekonany, ze tak by było dobrze to ok. Dziękuję za pomoc!