okrąg Fuerta: Dany jest trójkąt prostokatny ABC z katem prostym ACB. Niech r₁ oraz r₂ będą promieniami okręgów wpiasnych w trójkąty ACD oraz DCB, gdzie punkt D jest spodkiem wysokości z C na bok AB. Oblicz promień okregu wpisnego w trójkat ABC.

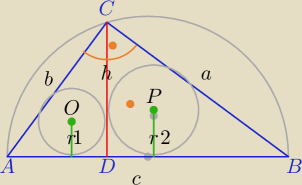
Mila: r− promień okręgu wpisanego w ΔABC

	b
1) ΔADC∼ΔACB w skali k=		⇔
	c

r1		b		r1*c
	=		stąd b=
r		c		r

	a
2) ΔCDB∼ΔACB w skali k=		⇔
	c

r2		a		r2*c
	=		stąd a=
r		c		r

3) w ΔACB:

	r2*c		r1*c
a2+b2=c2⇔ (		)2+(		)2=c2⇔
	r		r

r22		r12
	+		=1
r2		r2

r=√r₁²+r₂² ====================