Do pustej urny włożono 8 kul białych i 4 kule czarne, a następnie wylosowano bez
Mat: Do pustej urny włożono 8 kul białych i 4 kule czarne, a następnie wylosowano bez zwracania 5
kul. Jakie jest prawdopodobieństwo, że stosunek liczby kul białych do liczby kul czarnych w
urnie uległ zwiększeniu.
No więc omegę policzyłem tak:
Stosunek liczby kul białych do liczby kul czarnych zwiększy się, kiedy wylosujemy co najmniej 2
kule czarne, więc:
Wynik wychodzi mi zły, mógłby ktoś pomóc?
16 lis 19:49
Blee:
A jaki wychodzi prawidłowy wynik ?
Bo ja bym zrobił tak samo (w sensie ... uwzględniłbym kolejność, ale to nie odgrywa żadnej roli
tak naprawdę)
16 lis 19:56
16 lis 19:57
Tadeusz:
czyli 2 czarne lub 3 czarne (4 czarne odpada)
16 lis 20:00
Mat: Czyli wynik w książce jest zły. A więc jeśli wylosujemy 4 czarne to będziemy mieć 7/0 i w takim
wypadku nie pasuje to do zadania?
16 lis 20:05
16 lis 20:06
Mila:
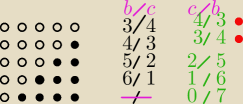
1) A− Stosunek liczby kul białych do liczby kul czarnych ulega zwiększeniu:
W przypadku ostatnim nie można określić wartości stosunku.
2)
B− Stosunek liczby kul czarnych do liczby kul białych ulega zwiększeniu:
Wylosowano 5 białych i ani jednej czarnej lub wylosowano 4 białe i jedna czarną.
16 lis 21:12
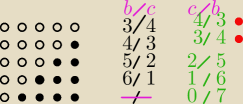 1) A− Stosunek liczby kul białych do liczby kul czarnych ulega zwiększeniu:
1) A− Stosunek liczby kul białych do liczby kul czarnych ulega zwiększeniu: