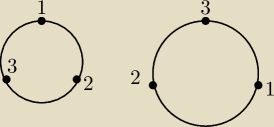
karuzela Krzysiek60: na ile sposobow mozna rozsadzic a) 3 osoby na 3 osobowej karuzeli b) 4 osoby na 4 osobowej karuzeli c) 5 osob na 5 osobowqej karuzeli d) n osob na n−osobowej karuzeli Uwaga : dwa rozsadzenia uwazamy za rozne jesli conajmniej jedna osoba ma conajmniej z jednej strony innego sasiada Takie zas rozsadzenia jak na rysunku sa identyczne (karuzela sie kreci Wiec tak jezeli bedziemy rozpatrywali funkcje roznowartosciowe to byloby a) 3! b) 4! c) 5! d) n! Tylko po co ta uwaga tutaj jest ?

Blee: a) , b) , c), d) <−−− źle tutaj KOLEJNOŚĆ na okręgu nie ma znaczenia (czytaj − miejsca NIE SĄ numerowane) Tak więc odpowiedzią będzie d) (n−1)! i wcześniejsze podstawiasz do tego wzoru. A w jaki sposób to zrobić ... otóż − pierwszy człowiek siada 'gdzie chce' −−− i go liczymy jako 1. Jak już usiadł to staje się naszym 'punktem odniesienia' więc od teraz pozostałe (n−1) miejsc na karuzeli już nie jest nierozróżnialna ... bo wiemy jakie jest położenie każdego miejsca względem tego pierwszego człeka. Stąd też posadzić n osób na n−osobowej karuzeli (częściej spotykane są zadania z okrągłymi stołami) można na (n−1)! sposobów.

Krzysiek60: Blee nie patrzylem do odpowiedzi i po prostu pomyslalem ze mamy tutaj permutacje ze zbioru n−elelentowego w zbior n elememtowy W odpowiedzi jest tak wlasnie jak piszsesz .dziekuje