daw
a47: Czy trójkąt o bokach 3,4,5 zawsze jest prostokątny?
15 lis 21:38
Krzysiek60: Tak
15 lis 21:38
the foxi:
niech α będzie kątem między bokami długości 3 i 4
z twierdzenia cosinusów:
3
3+4
2−2*3*4cosα=5
2, α∊(0;180
o)
25−24cosα=25
24cosα=0
α=90
o
innej możliwości nie ma

15 lis 21:49
Krzysiek60:
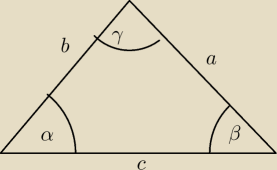
Twierdzenie
1) jesli w trojkacie c
2<a
2+b
2 to γ<90
o
2) jesli w trojkacie c
2= a
2+b
2 to γ= 90
o
3) jesli w trojkacie c
2>a
2+b
2 to γ>90
o
15 lis 22:15
Karolek : Oczywiście że tak nie ma innej opcji
16 lis 06:58
PW: 32+42=54, a więc trójkąt jest prostokątny (twierdzenie odwrotne do twierdzenia Pitagorasa).
Nawet najbardziej uroczyste zapewnienie, że "nie ma innej opcji" jest tylko zaklęciem, nie
dowodem.
16 lis 12:42
fsdgses: 32+52≠42
16 lis 12:44
Krzysiek60: O czym ty piszesz?
16 lis 12:47
jc: Na sferze to już nie będzie trójkąt prostokątny.
16 lis 12:50
Jerzy:
ln z liczb ujemnych też istnieje, ale raczej tutaj pytają o trójkąt na plaszczyźnie.
16 lis 12:53
PW: Korekta: o 12:42 napisane być powinno
3
2+4
2=5
2,
ale to chyba oczywiste. Przepraszam, takie błędy popełniam coraz częściej z powodu postępującej
utraty wzroku.
jc odpowiada na pytanie
a47, nie wpadłem na to, że uczeń średniej szkoły zadaje
"podchwytliwe pytania, na które nie zna odpowiedzi"

16 lis 13:03

 Twierdzenie
1) jesli w trojkacie c2<a2+b2 to γ<90o
2) jesli w trojkacie c2= a2+b2 to γ= 90o
3) jesli w trojkacie c2>a2+b2 to γ>90o
Twierdzenie
1) jesli w trojkacie c2<a2+b2 to γ<90o
2) jesli w trojkacie c2= a2+b2 to γ= 90o
3) jesli w trojkacie c2>a2+b2 to γ>90o
