niby wartość bezwzględna ale zadanie trudne... Ades: uzasadnij ze dla kazdej liczby x∊(−1,5) wyrażanie √4x2+12x+9 + 2√x2−12x+36 ma stałą wartość. W = 2*x + 3 + 2*(x − 6) = 2*x + 3 + 2*x − 12 = 4*x − 9 Natomiast rozwiązania poniższego nie rozumiem y = |2x + 3| + 2|x − 6| ⇒ y = 2|x +3/2I+2Ix−6I Dla x ∊ (−1, 5) ⊂ (− 3/2 , 6>: y = 2x + 3 − 2x + 12 ⇒ y = 15 co należało wykazać. Skąd minus przed 2x skoro był plus? Jestem w 1 LO

Krzysiek60: dla x∊(−1,5) |x−6|= −(x−6)= 6−x wstaw np sobie x=3 masz |x−6|= |3−6|= |−3|= −(−3)=3 zgodnie z definicja wartosci bezwzglednej i po zawodach

Jolanta: Przeciez ci napisałam

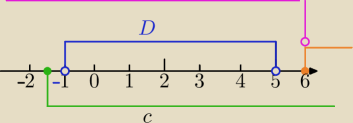
Mila: D=(−1,5) √4x²+12x+9 + 2√x²−12x+36 = =√(2x+3)²+2*√(x−6)²= =|2x+3| +2|x−6|

	3
|2x+3|=2x+3 dla 2x+3≥0⇔x≥−
	2

czyli w całym podanym przedziale (2x+3) ma wartość nieujemną |x−6|=x−6 dla x−6 ≥0⇔ x≥6 x−6 jest ujemne dla x<6 w takim razie |x−6| =−x+6 dla x <6 i również dla x<5 W=2x+3+2*(−x+6)=2x+3−2x+12=15 =========================== z def. |a|=a dla a≥0 |a|=−a dla a<0