| π | ||
sinx1= −1 to x= − | +2kπ ik∊Z | |
| 2 |
| 14 | ||
sinx2= | odpada bo sinx∊<−1,1> | |
| 4 |
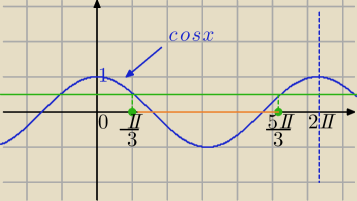
| π | 1 | |||
cos(2x− | )≤ | |||
| 3 | 2 |
| π | π | 5π | π | ||||
+2kπ≤2x− | ≤ | +2kπ / + | |||||
| 3 | 3 | 3 | 3 |
| 2π | 6π | ||
+2kπ≤2x≤ | +2kπ /:2 | ||
| 3 | 3 |
| π | |
+kπ≤x≤π+kπ | |
| 3 |
Pozdrawiam
Wlasnie niedwano wrocilem do domu
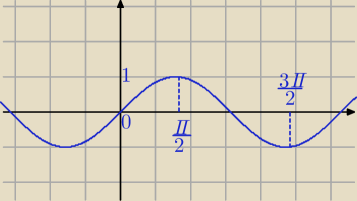2sin2x−5sinx −7=0
sinx=t, |t|≤1
2t2−5t−7=0
Δ=81
| 14 | ||
t=−1 lub t= | ∉D | |
| 4 |
| 3π | ||
x= | +2kπ, k∊C | |
| 2 |