Funkcje roznowartosciowe Inka: Wypisz wszystkie funkcje roznowartosciowe f: X→Y gdzie X={1,2,3} Y={a,b} Poprosze w miare o dokladne wytlumaczenie tego dlaczego takie funkcje nie istnieja . przeciez f(1)=a ≠ f(1)=b np

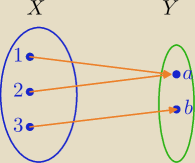
Mila: Każdemu elementowi ze zbioru X przyporządkowujemy dokładnie jeden element ze zbioru Y. Przykład: f(1)=a f(2)=a f(3)=b Dla dwóch różnych argumentów masz taka samą wartość.

Inka: dziekuje . Wiec jesli zbior X bedzie sie skladal z m elementow a zbior Y z k elemnetow i bedzie ze m>k to funkcji roznowartosciowych nie utworzymy Czy dobrze mysle ? Nastepna sytuacja X= {a,b} Y= {1,2,3} Byloby tutaj 6 funkcji roznowartosciowych Tylko znowu mam problem bo np dla argumentu a mamy 3 wartosci funkcji wiec to nie jest funkcja

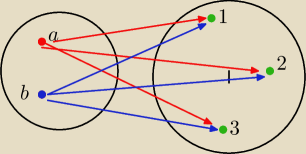
Mila: 22:01 ilustracja− To przyporządkowanie nie jest funkcją.

Inka: Ale mam w odpowiedzi ze jest 6 takich funkcji roznowartosciowych Wiec jak mam je wypisac ?

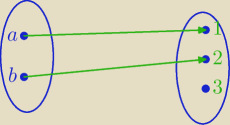
Mila: f: {a,b}→{1,2,3} Liczba funkcji różnowartościowych : 3*2=6 Ale ilustracja jest błędna> Jedna funkcja z tych 6 możliwych: 1) f(a)=1, f(b)= 2 ciąg (1,2) na ilustracji: Pozostałe: 2) f(a)=1, f(b)=3 ciąg (1,3) 3) f(a)=2, f(b)=1 ciąg (2,1) 4)f(a)=2, f(b)=3 ciąg (2,3) 5) f(a)=3, f(b)=1 ciąg (3,1) 6) f(a)=3,f(b)=2 ciąg (3,2)

Inka: Dziekuje . Musze to rozpracowac gdyz potem beda permutacje i pytaja o funkcje roznowartosciowe gdzie X={1,2,3} i Y= {a,b,c} tez wypisac

Mila: 3!=6 Najlepiej wypisz jako ciągi:

Inka: dziekuje za pomoc