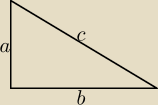
Trójkąt prostokątny Staś: W trójkącie prostokątnym długości boków są liczbami całkowitymi. Znajdź długości pozostałych boków jeśli jedna z przyprostokątnych ma 10 cm

PW: a=10, druga przyprostokątna to b, przeciwprostokątna to c. Zgodnie z twierdxeniem Pitagorasa a²+b²=c² 10² + b² = c² b² = c²−10² b•b = (c−10)(c+10) − pomyśleć jakie mogą być b i c, jeżeli są to liczby naturalne, przy czym c > 10 (przeciwprostokątna ma większą długość od boku a) i c>b.

Staś: próbowałem liczby do 30 nic nie wychodzi

Mila: To może tak: a²+10²=c² 100=c²−a² 100=(c−a)*(c−b) , c>a, c>0 i a>0 100=2²*5² 1) 2*50=(c−a)*(c−b) c−a=2 c+a=50 −−−−− + 2c=52, c=26, a=24 2) 100=4*25 c−a=4 c+a=25 2c=29 brak rozwiązań w zbiorze N₊

PW: Stasiu, najwyraźniej nie spróbowałeś c=26: b•b = 16•36 b•b = (4•6)(4•6)

Staś: Faktycznie pasuje, ale można by tak szukać w nieskończoność skąd wiedzieć ile ich jest

Bogdan: m, n ∊ N i m > n a = m² − n², b = 2mn, c = m² + n², są to znane zależności pozwalające wyznaczyć długości boków trójkąta prostokątnego z rodziny trójkątów pitagorejskich. Próbujemy: 2mn = 10 ⇒ mn = 5 ⇒ 5 * 1 = 5 a = 5² − 1² = 24, b = 2mn = 2*5*1 = 10, c² = 5² + 1² = 26. To jest trójkąt o bokach: 10, 24, 26