jd a47: boki trojkata maja 11 i 23 a srodkowa opuszczona na trzeci bok wynosi 10. Oblicz dlugosc trzeciego boku Nie wiem jak to zrobic z twierdzenia cosinusow, bo nie ma zadnego kąta podanego

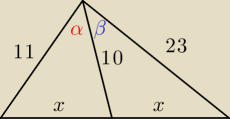
Blee: x² = 11² + 10² − 2*11*10*cosα x² = 23² + 10² − 2*23*10*cosβ (2x)² = 23² + 11² − 2*23*11*cos(α+β) gdzie cos(α+β) = cosαcosβ − sinαsinβ

Blee: albo: 10² = x² + 11² − 2*11*x*cosγ 23² = (2x)² + 11² − 2*11*(2x)*cosγ gdzie γ −−− kąt przy lewym wierzchołku

Blee: to drugie będzie łatwiejsze do przeliczenia

Blee: bo bardzo szybko można się pozbyć wyrażenia z cosinusem (wystarczy pierwsze równanie przemnożyć przez (−2) i dodać te dwa równania do siebie)

a47: dziena

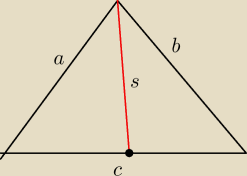
Inka: a=11 b=23 c? c²= 2(a²+b²−2s²)

a47: z czego wynika taka zależnosc?

the foxi: podejrzewam, że to przekształcenie wzoru na środkową trójkąta http://pl.wikipedia.org/wiki/Środkowa_trójkąta

Inka:

	1
s=		√2(a2+b2)−c2
	2

z tablic matematycznych

a47: hehe ciekawy wzor, uratowałby mnie na sprawdzianie ale trzeba bylo go znac

Blee: powyższy wzór wynika z 16:54, oto jak go wyprowadzić: s² = (c/2)² + a² − ac*cosγ //*(−2) b² = c² + a² − 2ac*cosγ + ______________________ −2s² + b² = c²/2 − a²

	1
s2 = −		(c2/2 − a2 − b2)
	2

	a2 + b2 − c2/2
s2 =
	2

	2(a2+b2) − c2
s2 =
	4

s = √(2(a²+b²) − c²)/4

	1
s =		√2(a2+b2) − c2
	2

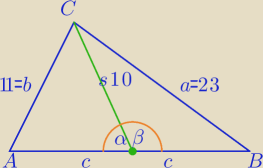Mila: a47 Trudno zapamiętać wszystkie wzory. Można tak: 1) cosβ=cos(180−α)=−cosα b²=c²+s²−2*c*s cosα i a²=c²+s²−2*c*s*cosβ 121=100+c²−2*c*10 cosα 529=100+c²+2*c*10 cosα −−−−−−−−−−−−−−−−−−−−−−−−−−−−− + 650=200+2c² 2c²=450 c²=225 c=15 |AB|=30 ========== 3)