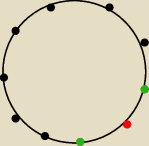
Przedszkolaki i ich okrągły stół Maciess: W pewnej grupie jest dwóch przedszkolaków, którzy się nie lubią oraz 8 dziewczynek. Oblicz na ile sposób można posadzić dziedzi przy okrągłym stole, tak aby chłopcy nie siedzieli obok siebie. Wybieram miejsce (czerwone) na 10 sposobów, dla drugiego nie moge na sąsiednich (zielone) czyli wybieram z 7.

10 1		7 1
	*		*8!=2822400 (?)

Pierwszy raz taki typ zadania spotykam (okrągły stół) i nie wiem czy czegoś nie pomijam.

Maciess: Refresh

Jerzy: Położenie czerwonej kropki jest bez znaczenia ( miejsca przy stole nie są numerowane) Patrz na rysynek i ustal ile dziewczynek mozesz wstawić w miejsce czerwonej kropki ( tutaj jest jedna dziewczynka ) i pamietaj,ze chlopców tez permutujesz.

Jerzy: I jescze jedno ... dla tego przypadku mamy: 8!*2!

Pytający: Jerzy, nie zrozumiałeś Maciessa − czerwona kropka oznacza chłopca, zielone kropki oznaczają jakieś dziewczynki. I okrągły stół nie musi oznaczać, że miejsca przy nim są nierozróżnialne. Okrągły stół wskazuje na cykliczność miejsc (ostatnie sąsiaduje z pierwszym, nie jak na ławce). Znaczy: • jeśli rozróżniamy miejsca przy stole (np. są ponumerowane), to szukanych rozsadzeń jest

	10 1	7 1
faktycznie			*8!=70*8!, jak w pierwszym poście. Ewentualnie można policzyć

(wszystkie rozsadzenia)−(rozsadzenia takie, że chłopcy siedzą obok siebie), czyli

	10 1
10!−		*2!*8!=70*8!,

	7 1
• jeśli nie rozróżniamy miejsc przy stole, to szukanych rozsadzeń jest		*8!=7*8!, bo

pierwszy chłopiec jest wtedy punktem odniesienia (pozostałych ustawiamy względem niego, na którymkolwiek miejscu siedzi). Inaczej 9!−2!*8!=7*8!.