prosta równoległa do prostej w 3d studenttt: prosta l1={x=1+4t&y=9+3t&z=3+t> t∊R leży w płaszczyźnie π, która jest równoległa do prostej l2=<x=4+3s&y=−10+2s&5−s> s∊R. Wybierz Odległość między prostymi $l₁$ i $l₂$ jest równa $10\sqrt{3}$. Płaszczyzna $\pi$ przechodzi przez punkt $(−6,4,3)$. Odległość prostej $l₂$ od płaszczyzny $\pi$ jest równa $10\sqrt{3}$. Płaszczyzna $\pi$ jest równoległa do płaszczyzny o równaniu $5x+7y+z+4=0$.

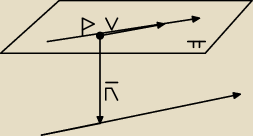
studenttt: Mam takie coś: z prostej l1 wyznaczam wektor v1=[4,3,1] i punkt p1=(1,9,3) jak wyznaczyć płaszczyznę π mając takie dane? Czy jest to możliwe? Dalej − jak wyznaczyć wektor normalny...? czy w ogóle dobrze rozumuję? Pozdrawiam

studenttt: https://snag.gy/dintIV.jpg Zadanie wygląda tak, jak w powyższym linku. Coś się stało i źle napisałem treść

studenttt: .

Mila: l₁: prosta leży w pł. π x=1+4t y=9+3t z=3+t, t∊R , A=(1,9,3) ∊π k₁^→=[4,3,1] wektor kierunkowy prostej l₁ l₂: x=4+3s y=−10+2s z=5−s, s∊R , B=(4,−10,5) ∊l₂ k₂^→=[3,2,−1] wektor kierunkowy prostej l₂ l₂ ||π −−−−−−−−−−−− 1) Równanie płaszczyzny π n^→=[4,3,1] x [3,2,−1]=[−5,7,−1] || [5,−7,1] n^→=[5,−7,1] i A=(1,9,3) ∊π 5*(x−1)−7*(y−9)+1*(z−3)=0 5x−5−7y+63+z−3=0 π : 5x−7y+z+55=0 2) P(−6,4,3) 5*(−6)−7*4+3+55=−30−28+58=0 P∊π 3) B=(4,−10,5) ∊l₂

	|5*4−7*(−10)+5+55|
d(B,π)=		=
	√52+72+12

	|20+70+60|		150		30
=		=		=		=10√3
	√75		5√3		√3

posprawdzaj rachunki i wybieraj odpowiedzi.

studenttt: rozumiem zatem, że odpowiedzi 1,2,3 są prawidłowe?

Mila:

studenttt: dzięki