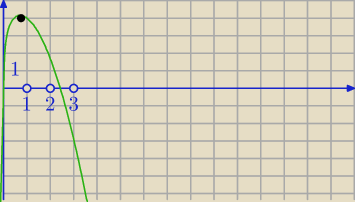
badanie przebiegu zmienności funkcji, studia gabrysia_12: 1. Wyznaczyć przedziały wypukłości, wklęsłośći oraz punkty przegięcia funkcji f(x)= e⁻2x+x⁴−3x+1 Druga pochodna wyszła mi 4e⁻2x+12x² i nie wiem jak wyzanczyć miejsca zerowe. Podpowie ktoś ? ps. tam jest e do potęgi −2x 2.Wyznaczyć przedziały wypukłości, wklęsłośći, punkty przegięcia i monotoniczność funkcji f(x)= lnx−x²+5 Wyszło mi, że druga pochodna nie ma miejsc zerowych i jest ujemna dla całej dziedziny, pierwsza pochodna zeruje się w −√2/2 i √2/2, jest dodatnia od 0 do √2/2, i ujemna od √2/2 do nieskończoności, w pkt x=0 funkcja osiąga max lokalne i punkt przegięcia

iteRacj@: 1/ 4e^−2x+12x²=0 e^−2x+3x²=0 e^−2x=−3x² lewa strona równania dodatnia ← → prawa strona równania niedodatnia (ujemna lub zero) brak miejsc zerowych, brak punktów przegięcia funkcji

iteRacj@: zad.2/ trzeba zacząć od dziedziny funkcji D=R₊ − dziedziny pochodnych muszą się zawierać w D, − 0 nie należy do dziedziny funkcji, więc nie należy do dziedziny pierwszej pochodnej D' ani do dziedziny drugiej pochodnej D" − nie ma tam ani maksimum lokalnego ani punktu przegięcia ani obu naraz (!)

gabrysia_12: Rzeczywiście zapomniałam spojrzeć na dziedznę. A co dzieje sie z punktem ^√2₂ ?

iteRacj@:

	√2
pochodna zmienia znak z dodatniego na ujemny więc dla x=		funkcja osiąga maksimum
	2

lokalne, to jest jedyne ekstremum lokalne tej funkcji, punktów przegięcia nie ma

gabrysia_12: Ok, dziękuję bardzo!😀