 Jeden ze sposobów : analitycznie
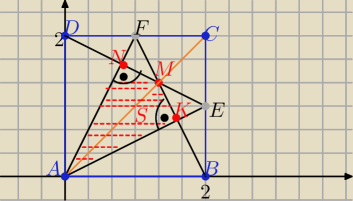
Umieszczamy kwadrat w układzie współrzędnych ( jak na rys.) o boku długości np: 2
A(0,0) , B(2,0), C(2,2),D(0,2), E(2,1), F(1,2)
równania prostych:
AC: y=x , AE: y=2x, DE: y=−0,5x+2
Rozwiązując układy równań:
Jeden ze sposobów : analitycznie
Umieszczamy kwadrat w układzie współrzędnych ( jak na rys.) o boku długości np: 2
A(0,0) , B(2,0), C(2,2),D(0,2), E(2,1), F(1,2)
równania prostych:
AC: y=x , AE: y=2x, DE: y=−0,5x+2
Rozwiązując układy równań:
| ⎧ | y=2x | ||
| N(x,y) : | ⎩ | y=−0,5x+2 |
| ⎧ | y=x | ||
| i M(x,y) : | ⎩ | y=−0,5x+2 |
| 4 | 8 | 4 | 4 | |||||
N( | , | ) i M( | , | ) | ||||
| 5 | 5 | 3 | 3 |
| 4√5 | 4√5 | |||
|MN|=...= | i |AN|= | |||
| 15 | 5 |
| 4√5 | 4√5 | 16 | ||||
S= 2P(ANM) = | * | = | i P(ABCD)=4 | |||
| 15 | 5 | 15 |
| 4 | ||
to S= | P | |
| 15 |
| 16 | ||
S= | a2 i P(ABCD)=4a2 | |
| 15 |
| 4 | ||
to S= | P | |
| 15 |
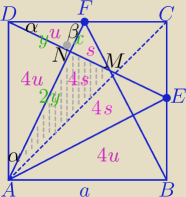 Do sposobu Ety dołączam II sposób z wykorzystaniem podobieństwa Δ.
P− pole kwadratu
Do sposobu Ety dołączam II sposób z wykorzystaniem podobieństwa Δ.
P− pole kwadratu
| 1 | ||
1)ΔDNF∼ΔDNA w skali k= | ( Δprostokątne podobne do ΔADF) | |
| 2 |
| 1 | 1 | |||
5u= | P ⇔u= | P | ||
| 4 | 20 |
| 1 | 4 | 1 | ||||
9s+4u= | P ⇔9s+ | P= | P | |||
| 2 | 20 | 2 |
| 1 | ||
s= | P | |
| 30 |
| 8 | ||
8s= | P | |
| 30 |
| 4 | ||
8s=PAEMN= | P | |
| 15 |

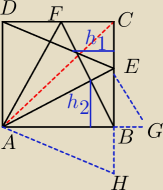 Dla uproszczenia opisów AB=1
DE || AH
FB || EG
Dla uproszczenia opisów AB=1
DE || AH
FB || EG
| h2 | 0,5 | 2 | |||
= | h2= | ||||
| 1 | 1,25 | 5 |
| h1 | 1 | 1 | |||
= | h1= | ||||
| 0,5 | 1,5 | 3 |
| h2 | h1 | 4 | ||||
P=1*1−2*1* | −2*1* | = | ||||
| 2 | 2 | 15 |