pilne makro: oblicz długość boku kwadratu wpisanego w trójkąt równoboczny o boku a

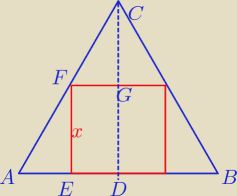
Basia: △AEF ∼△FGC AE = ^a₂−^x₂ = ^a−x₂ EF=x FG = ^x₂

	a√3−2x
CG = h−x = U{a√3}2}−x =
	2

AE		EF
	=
FG		GC

a−x2		x
	=
x2		a√3−2x   2

a−x		2x
	=
x		a√3−2x

(a−x)(a√3−2x) = 2x² a²√3−2ax−a√3x+2x²=2x² −2ax−a√3x = −a²√3 −ax(2+√3) = −a²√3

	−a2√3
x =
	−a(2+√3)

	a√3
x =
	2+√3

P = x² = U{3a²}{(2+√3))² =

3a2
	=
4+4√3+3

3a2
	=
7+4√3

3a2(7−4√3)
	=
(7+4√3)(7−4√3)

3a2(7−4√3)
	=
49−16*3

3a²*(7−4√3) o ile nie pomyliłam się w rachunkach

Basia: tylko długość boku czyli:

	a√3
x =		=
	2+√3

a√3(2−√3)
	=
(2+√3)(2−√3)

a√3(2−√3)
	=
4−3

a√3(2−√3)