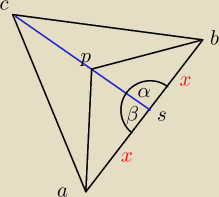
 Punkt P należy do środkowej CS trójkąta ABC. Uzasadnij, że pola trójkątów APC I PBC są równe.
Czy poniższy dowód jest poprawny?
|AS|=|BS|=x
β=180−α
Punkt P należy do środkowej CS trójkąta ABC. Uzasadnij, że pola trójkątów APC I PBC są równe.
Czy poniższy dowód jest poprawny?
|AS|=|BS|=x
β=180−α
| 1 | ||
PΔBCS= | x*|CS|*sinα | |
| 2 |
| 1 | 1 | |||
PΔACS= | x*|CS|*sin(180−α)= | x*|CS|*sinα | ||
| 2 | 2 |
| 1 | ||
PΔBPS= | x*|PS|*sinα | |
| 2 |
| 1 | 1 | |||
PΔAPS= | x*|PS|*sin(180−α)= | x*|PS|*sinα | ||
| 2 | 2 |
| 1 | 1 | |||
PΔBPC= | x*|CS|*sinα− | x*|PS|*sinα | ||
| 2 | 2 |
| 1 | 1 | |||
PΔAPC= | x*|PS|*sinα− | x*|PS|*sinα | ||
| 2 | 2 |
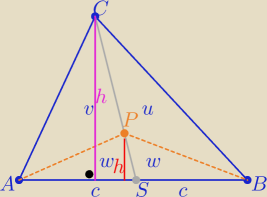 Każda środkowa dzieli trójkąt na dwa trójkąty o równych polach
zatem P(ASP)=P(BSP)= w
P(ASC)=P(BSC)
v+w=u+w ⇒ v=u ⇒ P(APC)=P(BPC)
c.n.w
Każda środkowa dzieli trójkąt na dwa trójkąty o równych polach
zatem P(ASP)=P(BSP)= w
P(ASC)=P(BSC)
v+w=u+w ⇒ v=u ⇒ P(APC)=P(BPC)
c.n.w
