. Karol: Oblicz promień okręgu wpisanego w trójkąt prostokątny, którego długości przyprostokątnych są dodatnimi pierwiastkami równania x² − 2p^x + 2p = 0

iteRacj@: czy może chodzi o równanie x² − 2px + 2p = 0 ?

Karol: Tak oczywiście, przepraszam, mój błąd

Jerzy: Zacznij od ustalenia p , dla którego to równanie ma dwa pierwiastki dodatnie.

Karol: I później co?

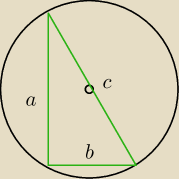
i: x²−2px+2p = 0 1/ jeśli masz już założenia, to je wpisz tutaj 2/ rozwiązania równania istnieją i są dodatnie oznaczamy je a i b, więc można skorzystać z tw.Pitaogorasa c=2r gdzie r szukany promień c²=a²+b²=(a+b)²−2ab 3/ zastosuj wzory Viete'a

	−2p		2p
(a+b)2−2ab=(		)2−
	1		1

4/ sprawdź, czy otrzymane rozwiązanie należy do dziedziny

i:

	2p		2p
w 3/ ...=(		)2−2
	1		1

Jerzy: Nie o to chodzi w tym zadaniu.

Karol: To w końcu jak?

Jerzy: Przecież to okrąg ma być wpisany w trójkąt, a nie odwrotnie.

i: sorry oczywiście, że nie okrąg ma być wpisany

i: *okrąg ma być wpisany w trójkąt a nie opisany na trójkącie jak u mnie

piotr: x²−2m x+2m=0 a=1 b=−2m c=2m Δ = −8 m + 4 m² {Δ≥0,−b/a>0, c/a>0} ⇒ m≥2

	2PΔ		c/a
r =		=		= m−√m(m−1)
	obwódΔ		−b/a+√(b/a)2−2c/a