kąty ABC: Na ramionach BC i AC trójkąta równoramiennego ABC wybrano odpowiednio punkty M i N tak że miary kątów |BAM|=|ABN|=|ACB| oraz zachodzi równość |AM|+|AB|+|BN|=|AC| Oblicz miary kątów tego trojkąta Mogę prosić o pomoc

Eta: 20^o,80^o,80^o ===========

ABC: ale jak do tego doszłaś ?

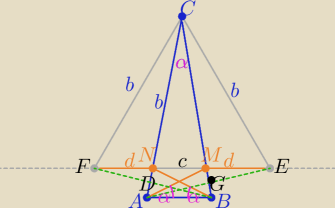
Eta: 1/ rys. zgodny z treścią 2/ odkładam na prostej MN odcinki d=|AM|=|BM| bo w treści mamy: |AM|+|NM|+|BN|= |AC| ⇒ |FE|= d+d+c= |AC| zatem otrzymujemy trójkąty AEC i BEC które są równoramienne i przystające o ramionach długości |AC|=b i wysokościach |CG|=|CD| to |<FCE|= 3α więc ΔEFC jest równoboczny o boku |AC| to 3α=60^o ⇒ α= 30^o skoro trójkąt ABC jest równoramienny to pozostałe dwa kąty przy podstawie mają miary po 80^o Odp: kąty trójkąta ABC : 30^o,80^o,80^o Może ktoś poda jeszcze inny sposób rozwiązania

Krzysiek60: Dobry wieczor 190^o>180^o

Eta: 3α=60^o to α=20^o ! ( tu się walnęłam Odp : 20^o,80^o,80^o =================== dzięki za poprawkę

Krzysiek60: 3α=60 α=20^o nie 30 ^o wiec mialas Eta dobrze 20,80,80

Mila: W treści z 20:36 jest podane: |AM|+|AB|+|BN|=|AC| To jak ma być? Autor milczy.