Zadanie z matury prosze o pomoc maryo: Zadanie 8 − matura 9 maja 2016 − rozszerzenie: Wykaż, że dla dowolnych dodatnich liczb rzeczywistych x i y takich, że x²+y²=2, prawdziwa jest nierówność x+y≤2. Gdzie robie błąd? Jak dla mnie to biore zaleznosc z rownania, ze 2=x²+y² i podstawiam to za 2 do nierownosci i wychodzi, ze suma kwadratow dwoch liczb dodatnich jest wieksza lub rowna sumie tych dwoch liczb, co sie zgadza, ale to byloby zbyt proste, dlatego co jest bledne w takim mysleniu?

Adamm: x+y≤x²+y² nie musi być prawdą weźmy x = y = 1/2

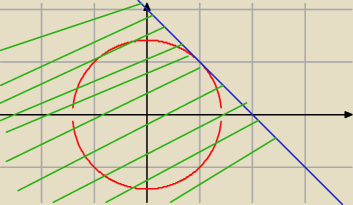
PW: Nierówność ma ładną interpretację geometryczną. Wszystkie punkty okręgu x²+y²=2 leżą poniżej prostej y=−x+2 oprócz punktu wspólnego (1, 1)

PW: Po lewej stronie okienka edycyjnego jest pierwszy od góry link Matura z Matematyki. Jeżeli szukasz rozwiązań zadań maturalnych, to zaczynaj od tego. W tym konkretnym wypadku dobrze jest zajrzeć do komentarzy, jest tam kilka rozwiązań innych od proponowanego przez Jakuba.

Mila: https://www.zadania.info/d1641/7019154