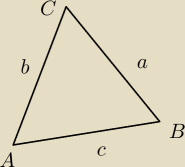
 Dany jest trójkat ABC tak jak na rysunku. Wiadmo że b*cos∡BAC−a*cos∡ABC=2c oraz
b2+c2=a2+√3bc. Oblicz długość a, jeśli pole trójkata wynosi √3.
Dany jest trójkat ABC tak jak na rysunku. Wiadmo że b*cos∡BAC−a*cos∡ABC=2c oraz
b2+c2=a2+√3bc. Oblicz długość a, jeśli pole trójkata wynosi √3.
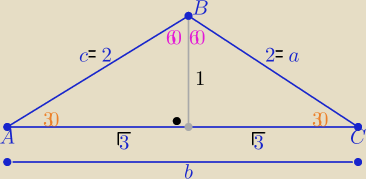 Wszystkie warunki zadania spełnia trójkąt ( podany na rys.)
ABC −− równoramienny o kątach 30o,30o, 120o
b= 2√3 , c= 2 ,a=2
Wszystkie warunki zadania spełnia trójkąt ( podany na rys.)
ABC −− równoramienny o kątach 30o,30o, 120o
b= 2√3 , c= 2 ,a=2
| 2√3*1 | ||
1/ P(ABC)= | =√3 ok | |
| 2 |
| √3 | 1 | |||
2/ b*cos30o−a*cos120o = 2√3* | +2* | = 3+1=4 =2c ok | ||
| 2 | 2 |
 Ano tak:
Ano tak:
| bc*sinα | ||
1/ P= | ⇒ bc*sinα=2√3 | |
| 2 |
| √3 | ||
to 2bc*cosα=√3bc ⇒ cosα= | ⇒ α= 30o | |
| 2 |
| √3 | ||
2bc* | −2ac*cosβ=4c2 ⇒ 12−2ac*cosα=4c2 | |
| 2 |