zadania optymalizacyjne julka.wawrzyniak: Suma długości wszystkich krawedzi ostroslupa prawidlowego czworokatnego jest rowna 24. Wyznacz dlugosc krawedzi podstawy takiego ostroslupa ktorego objetosc jest najwieksza.

DM: Czy odpowiedź to 10 + 2√13 ? xD

Mila: To niemożliwe, 4*10>24

DM: W sumie racja. Wyszła mi bardzo skomplikowana funkcja:

	1
V(x) =		x2√(6−x)2 − x22
	3

DM: Czy odpowiedź to 10 − 2√13 ?

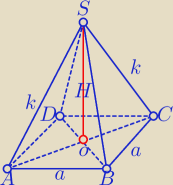
Mila: 1) 4a+4k=24 a+k=6 2)

	a√2
k=6−a i k>0 i H2+(		)2=k2
	2

	1		1
6−a>0 i H2=(6−a)2−		a2 stąd (6−a)2−		a2>0
	2		2

a∊(0,6) i [a<12−6√2 lub a>12+6√2 ]⇔ a∊(0,12−6√2) [12−6√2≈3.54] 3)

	a2*√0.5a2−12a+36
V(a)=
	3

Licz dalej sama pochodną i miejsca zerowe; mam wynik: a=10−2√13 [≈2.7888 ]

DM: To dobrze miałem

Mila: