Zadania optymalizacyjne diunaj: trójkąt równoboczny ABC ma bok długości 10 cm. Na jego bokach obrany punkty M,N,P tak, że |AM = |BN| = |CP| . Jak należy wybrać punkty M,N,P aby pole trójkąta MNP było najmniejsze

diunaj: Robiłem to w ten sposób i nie wychodzi: x + y = 10 => y = 10 − x

	MP2√3
PMNP =
	4

|MP|² + x² = y² |MP| = √ (10 −x)² − x² |MP| = √100 − 20x − a chyba powinno wyjść równanie kwadratowe, żebym mógł obliczyć wierzchołek, czyż nie?

diunaj: up

diunaj: upupupupupupupupup

diunaj: up

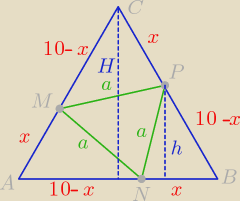
Godzio: Żeby Pole tego trójkąta było najmniejsze to Pola tych 3 trójkątów muszą być największe więc wysokość trójkącika:

H		10
	=
h		10−x

	10√3
10h =		* (10−x) /:10
	2

	√3
h =		* (10−x)
	2

	√3		√3		√3
Ptrójkącika = x * h = x *		* (10−x) = (10x − x2)*		= −		x2 +
	2		2		2

5√3x

	1
xw = −5√3 * (−		= 5
	√3

czyli punkty należy obrać na środkach boków trójkąta

diunaj: Dzięki, masz u mnie piwo x]

Godzio: