równania wymierne hubi:

x2−8x+6
	< 5
x2+2

No i udało mi się doprowadzić do formy:

−4x2−8x−4
	<0
x2+2

Tutaj się zaczynają problemy. Z nauczycielem robiliśmy tak, że mnożyliśmy licznik przez mianownik, wyznaczaliśmy miejsca zerowe, a następnie rysowaliśmy wszystko na osi x Problem w tym, że wychodzi mi inny wynik niż powinien XD (x²+2)(−4x²−8x−4)<0 miejsca zerowe: x=−√2 x=√2 x=−1 x=0 Powinno wyjść x należy do R \ {−1} a mi wychodzi że x(−nieskoń.;−√2) U (−1;0) U (√2;nieskoń.) help...

Inka: Ale zauwaz kolego ze x²+2 nigdy nie bedzie <0

Inka: Poza tym x²+2=0 to x²=−2 no i co ?

hubi: Dobra, zagapiłem się XD Ale ciągle pozostają 2 miejsca zerowe i według nich x będzie należał od minus nieskończoności do −1 oraz od 0 do nieskończoności

hubi: a nie znowu jestem debilem

hubi: jest jedno miejsce zerowe, przepraszam XD

hubi: wyliczyłem to, a potem zignorowałem XD

Inka: −4x²−8x−4= −4(x²+2x+1)= −4(x+1)²<0

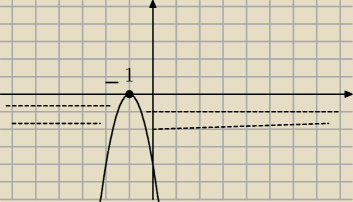
Inka: y=−4(x+1)² zeby bylo <0 musisz wylaczyc x=−1

Mila:

x2−8x+6
	<5 /*(x2+2) ( mianownik>0)
x2+2

x²−8x+6<5x²+10⇔ 4x²+8x+4>0 /:4 x²+2x+1>0 (x+1)²>0 dla x∊R\{−1}