Środkowe trójkąta. jaceksz73: Środkowe trójkąta mają długości 15, 36 i 39. Oblicz pole tego trójkąta. Bardzo zgrabnie sformułowane zadanie. Padło w zeszłym roku na konkursie gimnazjalnym. Jakubie warto dodać to zadanie do zadań o środkowych.

moze pomoge: a widze, ze wystarczy podstawic do wzoru

Inka: s₁= 15 s₂= 36 s₃= 39

	s1+s2+s3
p=
	2

	4
S=		√p(p−s1)(p−s2)(p−s3)
	3

Zauwzyc prosze ze podobny do wzoru Herona gdy masz boki Zostalo tylko podstawic i policzyc

Burczyk: Skąd się wziął ten wzór?

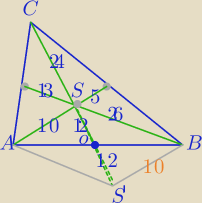
Mila: 1) Środkowe Δ przecinają się w jednym punkcie i dzielą w stosunku 2:1 licząc od wierzchołka Δ. 2) S' symetryczny do S względem punktu O. Czworokąt AS'BS jest równoległobokiem⇒|S'B|=10 3)

	24+10+26
p=		=30
	2

P_ΔSS'B=√30*(30−24)*(30−26)*(30−10)=120 4) P_ΔABC=3*120=360 ==================

jaceksz73: Dziękuję Mila. Bardzo klarowne i krótkie rozwiązanie. Inka: nie znałem tego wzoru. Gdzie go znalazłaś?

Krzysiek60: taki wzor jest w tablicach matematycznych

Krzysiek60: https://naforum.zapodaj.net/96f7634fe1ae.jpg.html https://naforum.zapodaj.net/28fc034b41f8.jpg.html https://naforum.zapodaj.net/f0b36511cf86.jpg.html https://naforum.zapodaj.net/b2fc3386e094.jpg.html