ós liczbowa Zielona: zaznacz na osi liczbowej |x|>0 albo poprosze tylko podać xe

Inka: Ta nierownosc jest prawdziwa dl x∊(−∞,∞)

the foxi: Inka, oprócz zera

Inka: Racja .

Ajtek: Inka, zastanów się dobrze.

Zielona: czyli (−∞,0) u <0,+∞)

Zielona: ?

Ajtek: (−∞;0)u(0;∞)

Zielona: a nie jest tak, ze przy takiej samej liczbie sie nie zmienia znak?

Inka: |x|=x dla x≥0 = −x dla x<0

Ajtek: Akurat nie w tym przypadku, tutaj masz nierówność ostrą. 0 nie jest większe od 0, zatem musimy je wywalic z rozwiązania.

Zielona: co to znaczy nierownosc ostra?

Ajtek: > lub <, nierówność słaba to ≥ lub ≤

Zielona: czyli przy slabej bylyby rozne?

Ajtek: Przy słabej przedział by był x∊R w tym przypadku. Domykanie nawiasów stosuję się w zadaniach typu: |x+2|±|x−3|≥0 ← to jest przykład tylko.

Ajtek: Ewentualnie |x−3|≥0

Zielona: ok, chyba rozumiem, dziekuje ^^

aa:

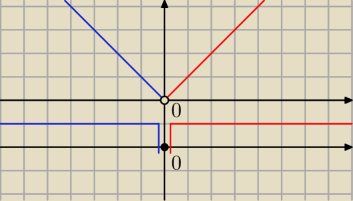
	⎧	−x dla x<0
|x| =	⎩	x dla x≥0

|x| > 0 dla: − x<0 −x > 0 x < 0 x ∊ (−∞, 0) − dla x≥0 x > 0 x ∊ (0, +∞) x ∊ (−∞, 0)∪(0, +∞)

Jerzy: Wszystkie liczby oprócz: x = 0.