Płaszczyzna zespolona - równania UczącySię: Na płaszczyźnie zespolonej zaznaczyć zbiór: E = { z ∊ℂ : Re(z²) = 2 ⋀ (Im(z+i))² = 1 } z = a + bi Więc z pierwszego: a² − b² = 2 Z drugiego: b² + 2b = 0 ... Nie wiem co dalej szczerze mówiąc, czy to rozwiązywać czy nie Drugi przykład:

	1
B = { z ∊ℂ : |z−i| ≤		}
	2

	1
|a + i(b−1)| ≤
	2

	1
√a2 + (b−1)2 ≤
	4

	1
a + b − 1 ≤		. Tu również nie wiem co dalej. Ponadto mam pytanie, bo wiem że w drugim
	4

przykładzie przy wartości bezwzględnej przy podniosłem do kwadratu i spierwiastkowałem został znak + a przecież i² = −1 ... Dlaczego tak Bardzo proszę o pomoc, jakąś podpowiedź

jc: Jak można pisać takie bzdury? √5=√4+1=2+1=3 ?

UczącySię: No właśnie dlatego dopytałem z tym drugim przykładem, bo na zajęciach tak zrobiliśmy ... W pierwszym chyba nie ma bzdur ?

jc: Nauczyciel zasnął?

UczącySię: A czy w pierwszym wyjdzie b = 0 i wtedy a = √2 lub a = −√2 Albo b = −2 i wtedy a = √6 lub a = −√6

UczącySię: No nie wiem, ale przyrzekam, że tak zrobiliśmy ... no cóż, zapytam dopiero w czwartek

Mila: B:

	1		1
|z−i|≤		− koło o środku S=(0,1) i r=
	2		2

jeżeli podstawimy: z=a+b*i, a, b ∊R to mamy:

	1
|a+bi−i|≤		⇔
	2

	1
|a+i*(b−1)|≤		⇔
	2

	1
√a2+(b−1)2≤		/2
	2

	1
a2+(b−1)2≤		i to jest koło jak podałam wyżej
	4

UczącySię: A więc, jc ... jednak nie pisałem bzdur tylko zapomniałem o kwadratach ... mój błąd Milu, bardzo dziękuję ! A czy zbiór E (przykład pierwszy) to będą te 4 punkty ?

Mila: Nie wiem, czy ma być : Im(z+i)² czy [Im(z+i)]²

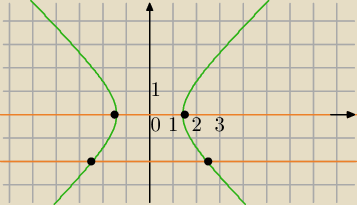
Mila: Lepiej zapisuj : z=x+iy E = { z ∊ℂ : Re(z²) = 2 ⋀ (Im(z+i))² = 1 } Re(z²)=2 z=x+y*i , x,y∊R z²=(x+yi)²=x²+2xy*i+(yi)²=x²+2xy*i−y² ( i²=−1) z²=(x²−y²)+2xy *i Re(z²)=x²−y² x²−y²=2 hiperbola i Im(z+i) = 1 z+i=x+i y+i z+i=[x+i*(y+1)] im(z+i)=(y+1) (y+1)²=1⇔ y+1=1 lub y+1=−1 y=0 lub y=−2 x²=2 ⇔Punkty: (√2,0) lub (−√2,0) lub y=−2 x²−4=2 ⇔x=√6 lub x=−√6 (√6,−2), (−√6,−2)

Mila: Jeżeli będziesz tak pisał jak wyżej, 21:49 , to oblejesz każde kolokwium. JC ma rację.

UczącySię: Uważam, że w pierwszym napisałem dobrze, a w drugim się pomyliłem