pole mat: Oblicz pole trójkąta ostrokątnego ABC w którym : podstawa |AB|=5, wysokość |AE|=4, środkowa |BE|=4,5

Inka : Tak nie moze byc .

mat: przepraszam środkowa |BD|=4,5 Teraz pomożesz ?

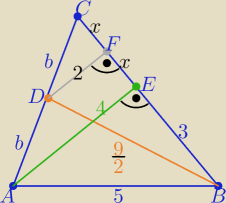
Eta: 1/ rys. zgodny z treścią zadania 2/ z tw.Pitagorasa w ΔABE .... |BE|= 3 3/ dorysowujemy odcinek DF ∥AE to z tw. Talesa .... |DF|=2 4/ z tw. Pitagorasa w ΔBDF

	81−16
(x+3)2=(9/2)2−22 ⇒ (x+3)2=		⇒ 2x+6=√65 to |BC|=3+2x ⇒|BC|=√65−3
	4

	1
P(ABC) =		*|BC|*|AE|
	2

P(ABC)=2(√65−3) [j²] ===================

mat: Teraz wszystko jasne i proste Wielkie dzięki Eta

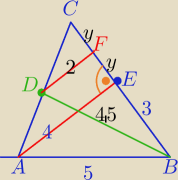Mila: Oblicz pole trójkąta ostrokątnego ABC w którym : podstawa |AB|=5, wysokość |AE|=4, środkowa |BD|=4,5 |BD|=4.5 |BE|=3 2) DF ||AE DF− odcinek łączący środki boków ΔAEC⇒|DF|=2 3) W ΔDFB: 4.5²=2²+(y+3)² 20,25−4=(y+3)² y+3=√16,25

	√65
y=		−3
	2

	√65
|BC|=2*(		−3)+3=√65−6+3=√65−3
	2

	1
4) PΔABC=		*(√65−3)*4
	2

P_ΔABC=2*(√65−3) ================= Posprawdzaj rachunki.

Mila: No to spóźniłam się