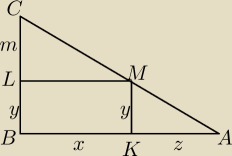
Udowodnij, że U{|BL|}{|BC|} + U{|BK|}{|BA|} = 1. Mat: W trójkąt prostokątny ABC o przeciwprostokątnej AC wpisano prostokąt KBLM w sposób pokazany na

	|BL|		|BK|
rysunku obok. Udowodnij, że		+		= 1.
	|BC|		|BA|

Poprosiłbym o weryfikację mojego rozwiązania. To x między np. |BL| i |BA| to mnożenie, potem po przejściu na literki oznacza niewiadomą.

|BL|		|BK|
	+		= 1
|BC|		|BA|

|BL|x|BA|+|BK|x|BC|
	= 1
|BA|x|BC|

|BL|x|BA|+|BK|x|BC|=|BA|x|BC| |BL|x|BA|+|BK|x|BC|−|BA|x|BC|=0 |BA|(|BL|−|BC|)+|BK|x|BC|=0 (x+z)(y−y−m)+x(y+m)=0 −xm−zm+xy+xm=0 xy−zm=0 xy=zm Z tw. Talesa:

y+m		x+z
	=
y		z

yz+mz=xy+yz mz=xy

	xy
m=
	z

xy=zm

	zxy
xy=
	z

xy=xy cnd.

Blee: Pytanie sprawdzające −−− dlaczego możesz skorzystać z tw. Talesa Wskaż mi w swoim rozwiązaniu miejsce w którym wykazujesz, że możesz z tegoż twierdzenia skorzystać.

Mat: A jeśli udowodnię, że mogę skorzystać z tw. Talesa lub zamiast tego posłużę się podobieństwem trójkątów ABC i AKM to rozwiązanie będzie dobre?

iteRacj@: proponuję wyjść od założeń i dojść do tezy, a nie odwrotnie zacznij od wypisania założeń |<CBA|= 90^o, LM||KB, |LM|=|KB|, LB||MB, |LB|=|MB| z tego wynika ΔCLM∼ΔMKA∼ΔCBA

m		y		m+y
	=		=
x		z		x+z

stąd xy=mz oraz y(x+z)=z(m+y)

y(x+z)
	=1
y(x+z)

z(m+y)
	=1
y(x+z)

zm+zy
	=1
y(x+z)

zm		zy
	+		=1
y(x+z)		y(x+z)

xy		zy
	+		=1
y(x+z)		z(m+y)

x		y
	+		=1
(x+z)		(m+y)

i to jest już teza

Eta: Z podobieństwa trójkątów ABC i AKM z cechy (kkk)

MK		AK
	=		i |MK|=|BL| i |AK|=|AB|−|BK|
BC		AB

	|BL|		|AB|−|BK|		|BL|		|BK|
to		=		⇒		=1−		⇒ ..... teza
	|BC|		|AB|		|BC|		|AB|

szymNski: αααααββββββγγγγγδδδδδπππππΔΔΔΔΔΩΩΩΩ∞∞∞∞∞∞