funkcja
wigle: jak wykazac ze funkcja f(x) = (x−5)
3+2 jest roznowartosciowa

2 lis 20:28
Blee:
z definicji
lub jak znasz pochodne to pokaż monotoniczność funkcji oraz jej ciągłość
2 lis 20:42
Eta:
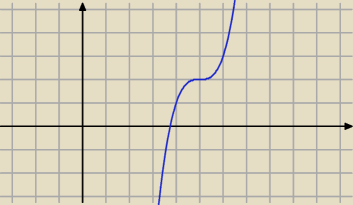
ściśle rosnąca więc .... różnowartościowa
2 lis 20:49
Adamm:
@Blee
co ty masz z tą ciągłością
2 lis 20:53
Eta:
"ciągłość umysłu"

2 lis 20:54
wigle: tylko w jaki sposob wykazac ze [(x1−5)
2 +(x1−5)(x2−5) + (x2−5)
2] jest zawsze rozne od zera

2 lis 21:27
jc: 0=a2+ab+b2=[a2+b2+(a+b)2]/2
gdyby a≠0 lub b≠0, to mielibyśmy liczbę dodatnią.
Zatem a=b=0.
2 lis 21:50
Mila:
Wykaż, że :
g(x)=x3 jest funkcją różnowartościową− to jest proste do wykazania
Po przesunięciu wykresu funkcji g(x) o wektor [5,2] mamy:
f(x)=g(x−5)+2 =(x−3)3+2 też jest f. różnowartościową,
2 lis 22:18

 ściśle rosnąca więc .... różnowartościowa
ściśle rosnąca więc .... różnowartościowa

