Uklad Inka : Dla jakich wartosci parametru p uklad rownan {x²+y²−2x=1 {y−x=p jest ukladem spraecznym y=p+x x²+(x+p)²−2x−1=0 2x²+2xp+p²−2x−1=0 2x²+(2p−2)x+p²−1=0 Δ= (2p−2)²−4*2(p²−1) Δ= 4p²−8p+4−8p²+8= −4p²−8p+12 <0 4p²+8p−12>0 p²+2p−3>0 Δ= 16 p₁= −3 p₂= 1 p∊(−∞,−3)U(1,∞) Sprawdzi ktos ?

iteRacj@: tak, dla takich wartości parametru okrąg i prosta nie mają punktów wspólnych

Inka : Dzięki

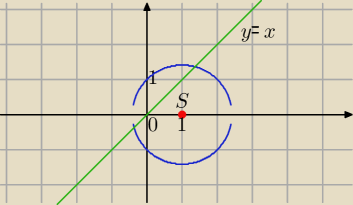
Mila: II sposób x²+y²−2x=1 i y−x=p (x−1)²+y²=2, S=(1,0) , r=√2 k: −x+y−p=0 d− Odległość S=(1,0) od prostej k większa od √2

|−1−p|
	>√2
√2

|p+1|>2 p+1>2 lub p+1<−2 p>1 lub p<−3 ============

Inka : Dzieki